Labb 1: Intro till Java utan objekt
Introduktion
Förberedelser
Gå på introföreläsningen. Börjar du tidigare gör du det "på egen risk".
Läs om grupper och handledning, och anmäl dig i WebReg.
Starta utvecklingsmiljön IDEA och konfigurera den för kursen.
Konfigurera versionshanteringen och skapa ett projekt i IDEA.
Här ger vi ett första smakprov på programmering i Java och programmering med statiskt typade variabler. Vi börjar med enklare uppgifter utan objektorientering, för att ge en grund i det som skiljer sig från t.ex. Python. Detta är ett direkt önskemål från tidigare studenter.
Vi vill också introducera utvecklingsmiljön, så ni hittar funktionalitet som tidigare studenter har haft mycket nytta av. Det sparar tid i det långa loppet.
Labbarna har relativt detaljerade instruktioner, som är integrerade med studiematerial som diskuterar bakgrunden till vad man gör. Det är ett medvetet grepp för att ni ska få lära genom att göra, istället för att ni får höra allt teoretiskt på föreläsningar och sedan omedelbart förväntas kunna applicera kunskaperna i praktiken.
Större stycken av studiematerial ligger i egna "rutor" medan enskilda fakta istället kan vara integrerade i själva uppgifterna.
Vägen är målet!
Vill kursledningen desperat ha 160 nästan identiska program som hälsar världen och som summerar, multiplicerar och hittar primtal? Nej, givetvis inte. Slutresultatet är alltså inte en uppsättning små program, utan består av kunskap, förståelse och färdigheter. Programmen finns där för att du ska få undersöka vägen som leder till en viss enkel funktionalitet.
Därför ger vi en hel del information som egentligen inte behövs för att man ska skriva rätt kod: Diskussioner av sammanhang, text som visar varför man gör på ett visst sätt, som generaliserar från nuet till det du kommer att ha nytta av i framtiden. Ta dig tid att läsa och reflektera!
Efter föreläsning 1, intro till Java
Uppgift 1.1: Ett första program
Syfte: Komma igång!
Nu vill vi så snabbt som möjligt skriva och köra ett första Java-program. Vi börjar därför med en enkel "Hello World" och förutsätter att du har gått genom förberedelserna överst på sidan.
Att förstå: Skapa paket och klass
Java kräver att man alltid "kapslar in" sin kod i en klass. Trots att vi
egentligen inte fokuserar på objektorientering behöver vi ändå börja med
att skapa klassen Exercise1.
För att organisera klasser, och undvika namnkollisioner när flera vill
använda samma namn, använder Java hierarkiska
paket, packages. Alla klasser i den här labben läggs i
paketet se.liu.ida.dinadress.tddd78.lab1, där
dinadress är din epostadress på formen noone123.
En katalogstruktur matchande paketnamnet kommer att skapas, där varje punkt i namnet anger en ny katalognivå. IDEA kan dock visa paket ihoptryckta så att "tomma mellannivåer" göms i projektvyn. Detta och andra inställningar sköts via kugghjulet överst i vyn.
Att göra: Skapa paket och klass
Skapa ett paket genom att högerklicka på src som ligger
under modulen lab1 i projektbrowserns hierarki. Att
ikonen för src är blå indikerar att den är en
källkodsmapp. Välj därefter New |
Package och skapa
paketet se.liu.ida.dinadress.tddd78.lab1.
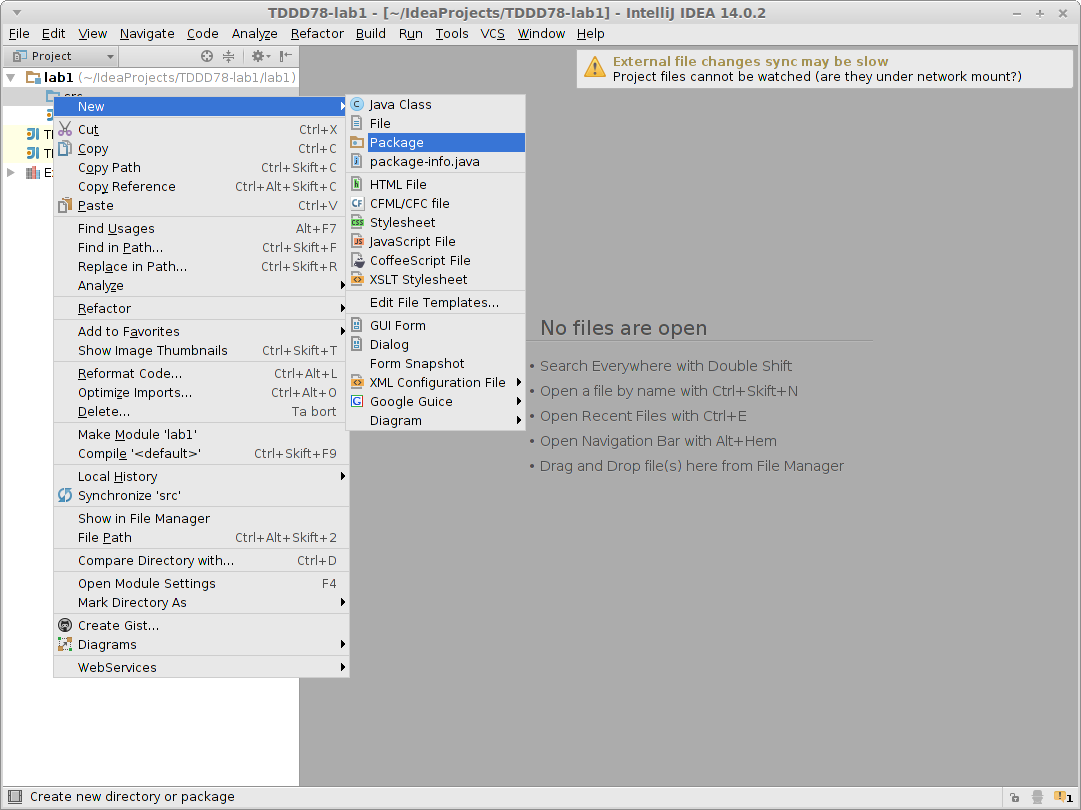
Skapa sedan klassen Exercise1 genom att högerklicka
på paketet (lab1) och välja New | Java
Class för att skapa klassen. Du anger bara
Exercise1, men det fulla namnet för klassen inklusive paket
blir
se.liu.ida.dinadress.tddd78.lab1.Exercise1. Klassen
skapas med attributet public vilket betyder att kod i
alla klasser kan komma åt den. Mer info om åtkomsträttigheter
kommer under föreläsningarna.
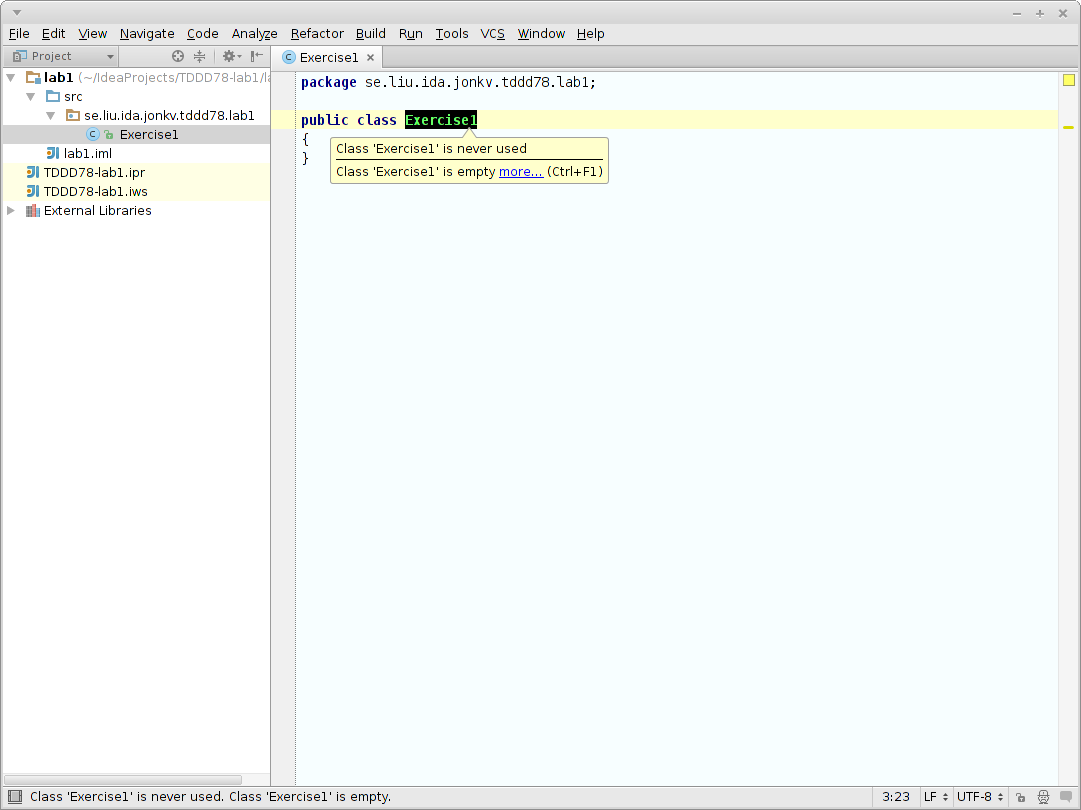
Att förstå: Varför så konstiga färger i IDEA?
Nu har "skelettet" till en klass skapats, men en del färger kan se lite
underliga ut. Klassnamnet "Exercise1" kan till exempel visas
i underliga färger. Varför då?
Pekar du på färgläggningen får du svaret: IDEA har upptäckt att du har en klass som aldrig används, och att den är tom. Detta är två av hundratals olika varningar som IDEA kan ge.
Ibland, som nu, kommer en varning helt enkelt för att vi inte har hunnit skriva klart.
Ibland kan det hända att vi har använt koden tidigare men slutat med det, och då är varningen bra att ha.
Ibland upptäcks allvarligare problem där varningarna kan vara livräddare.
-
Och ibland är varningarna helt enkelt felaktiga, eftersom analysen aldrig kan ha full förståelse av hur koden är tänkt att användas. "I genomsnitt" brukar varningarna dock ge mycket hjälp med många typer av problem.
Att förstå: Skapa huvudmetod
I ett enkelt "Hello World"-program behöver vi inga objekt, men vi
behöver veta vilken kod som körs när ett visst program
startas. Python kör all kod som är på "toppnivå" i den Python-fil
man anger. I Java anger man istället en klass, och en
speciell main-metod (funktion) i den klassen startas.
Metoden måste ha en specifik signatur (parametrar, returvärden,
...) för att bli igenkänd.
Att göra: Skapa huvudmetod
Skriv ett litet Hello World-program enligt bilden nedan.
Man kan med fördel använda IDEAs Live Template-funktion
genom att ställa markören i klassen (inom måsvingarna),
välja Code | Insert Live Template:
Ctrl-J , och sedan välja main() method
declaration. Ett ännu snabbare alternativ är att
skriva psvm och trycka Ctrl-J eller Tab. Det samma
gäller System.out.println(); som kan fås
via sout.
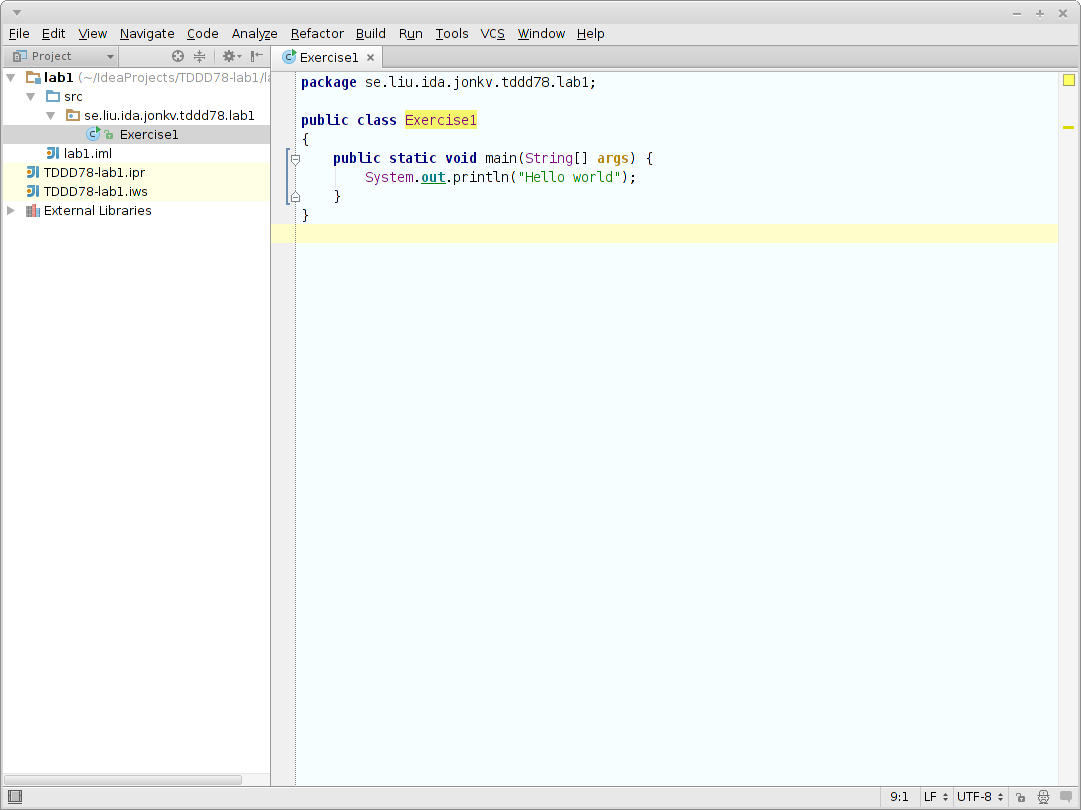
Som synes fick "Exercise1" nu en annan färg, eftersom vissa
varningar försvann (klassen är inte tom och den kan användas genom
att main() anropas) medan andra tillkom. I labb 1 kan ni ignorera
de flesta varningarna eftersom de gäller sådant vi ännu inte har
diskuterat.
Att förstå: Köra programmet
Vi ska nu köra programmet.
Precis som Python behöver Java först kompilera källkodsfilerna och
översätta dem till ett
internt bytekod-format.
I Python görs detta automatiskt "bakom kulisserna" av det
vanliga python-kommandot. Java har istället ett
separat kompileringssteg (kommandot javac) som bara
sparar den genererade bytekoden i form av .class-filer. Efter
kompilering kör man programmet med t.ex. "java
se.liu.ida.dinadress.tddd78.lab1.Exercise1".
IDEA tar dock hand om kompileringssteget automatiskt när man vill starta ett program.
Att göra: Köra programmet
Högerklicka någonstans i den öppna filen och välj Run Exercise1.main(). Detta kompilerar automatiskt alla okompilerade filer, verifierar att inga kompileringsfel uppstod, och startar det program vi högerklickade. Du bör se utskriften i IDEAs körfönster:
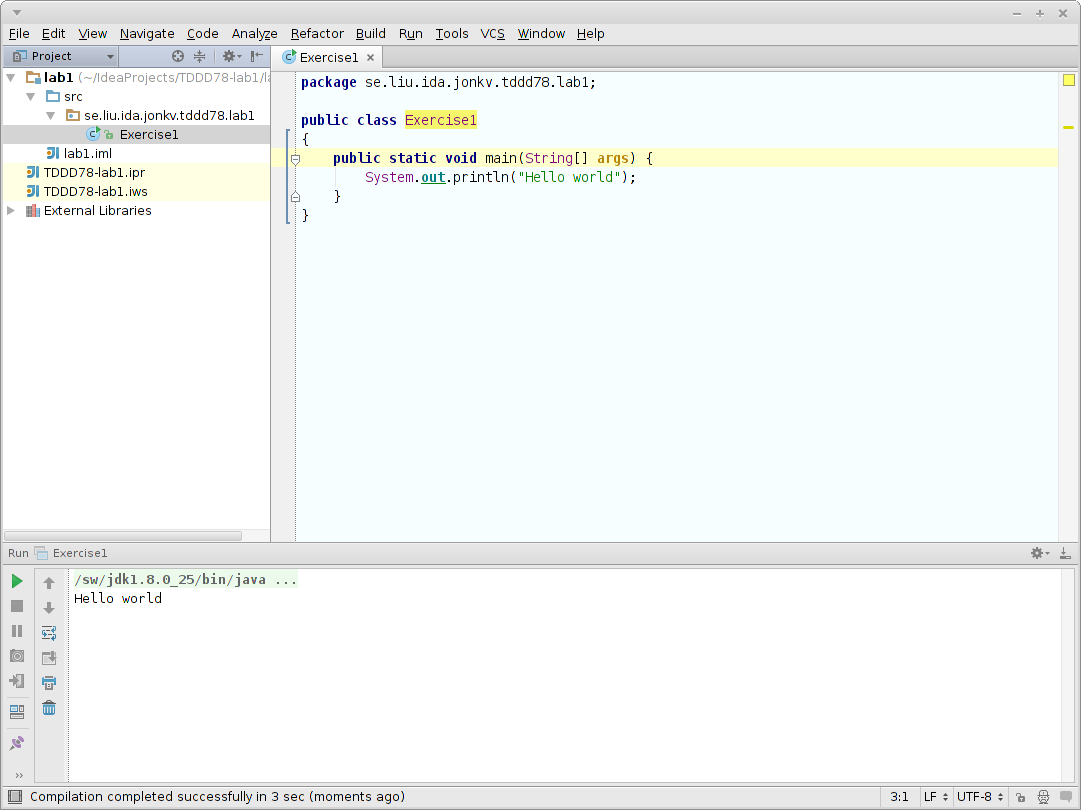
Då man kör programmet skapar IDEA en körkonfiguration. Man kan välja bland körkonfigurationer och köra dem enkelt via knappmenyn (toolbar), och editera dem för att t.ex. lägga till kommandoradsparametrar. Om det inte syns en knappmeny i IDEA kan denna tas fram genom View | Toolbar.
Verktyg: Kompilera utan att köra (IDEA)
IDEA kompilerar som sagt automatiskt innan ett program startas, men ibland vill man kompilera utan att köra, t.ex. för att dubbelkolla att inga syntaxfel finns kvar. Detta görs genom:
Build | Make Project Ctrl-F9, som kompilerar "det som behövs" men behåller det som inte ändrats.
Build | Rebuild project, som rensar gamla resultat och sedan kompilerar allt.
Uppgift 1.2: Kontrollstrukturer
Syfte: Bli bekant med kontrollstrukturer
Java har flera olika kontrollstrukturer för iteration (upprepning). Tidigare studenter har önskat sig övningar på detta, för att bekanta sig med alla och se hur de fungerar.
Att göra: Skapa ny klass
I labb 1 skapar vi oftast en ny klass för varje uppgift. Här skapar du
klassen Exercise2 i det paket du skapade tidigare. Klassen
kan skapas:
- (a) på samma sätt som förut genom att högerklicka på paketet (lab1) och välja New | Java Class, eller
- (b) genom att ställa markören på klassnamnet
Exercise1, trycka F5 (clone) och svara på frågorna.
I det senare fallet behöver man också ta bort onödig kod i den nya klassen – eller kommentera bort den, om man tror att den snart ska användas igen. IDEA underlättar att kommentera bort kodavsnitt genom att man markerar dem och trycker CTRL-/.
Att förstå: Summera tal med for-loop
Här börjar vi med en for-loop. I Java har den samma "format"
som i till exempel C, C++, JavaScript, Perl och PHP, med följande syntax:
for (initialization; condition; increment) {
statements
} - Initialization
Här deklareras och initialiseras den räknare som vi använder. Som alltid i Java måste man ange variabelns typ vid deklarationen. Exempelvis:
int i = 1omiär en tidigare okänd variabel som vi vill använda som räknare. Vi använder ofta justi,j,ksom loopvariabel när vi har en kort loop och bara vill räkna antal gånger loopen körs. Om variabeln betyder något mer, döper vi den så att den blir mer förståelig (x, pos, cardNumber, enemyIndex, ...).- Condition
- Här beskrivs det villkor som måste vara uppfyllt för att iterera ett varv (till). Exempelvis:
i < 10. - Increment
- Här anges hur räknaren skall uppdateras. Exempelvis:
i++(som betyder samma somi+=1).
Ett fullständigt exempel för att iterera 10 gånger ser ut så här:
int a = 42;
for (int i = 0; i < 10; i++) {
a = a + 20;
System.out.println("Nu har a värdet " + a);
}
Detta är det kanoniska (vanliga, standardiserade) sättet att
loopa över ett intervall av heltal i Java, C, C++ med mera, till skillnad
från Python som använder sin range-funktionalitet.
När koden exekveras:
Först kommer initialization att köras. Det betyder att det kommer att finnas en int-variabel med namn
ioch värde 0 ifor-loopen.Innan varje iteration av koden i loopen, inklusive den första, kontrolleras condition-villkoret. Om det är falskt avbryts loopen. Annars exekveras den inre koden en gång. I det här fallet kommer värdet på variabeln
aatt ökas med 20.När koden i
for-loopen har exekverats anropas increment-koden som i detta fall räknar upp värdet påimed 1. Därefter sker nästa test av condition, och så vidare.
a med 20.
Alla variabler har ett scope, en "räckvidd", som anger var de är tillgängliga. Detta scope kan fungera olika i olika språk.
I Java blir en variabel som deklareras inuti ett {block}
bara tillgänglig inuti detta block. När man "går ut" en nivå är variabeln
"borta".
Det gäller även variabler som deklareras inuti själva for-satsen.
Därför är variabeln i ovanför bara känd i for-loopen
och kan inte användas efter loopen. Det går däremot bra
att återanvända namnet till andra variabler efter loopen.
Att göra: Summera tal med for-loop
-
Skriv en funktion
sumFor(int min, int max)som beräknar och returnerar summan av talenmin,min+1,...,maxmed hjälp av enfor-loop. -
Skapa en
main()-funktion.Vi vill vänta lite till med att titta på hur man hämtar input från användaren. Vi börjar därför med att hårdkoda värden på min och max. Vi kommer senare att läsa in dessa från användaren. Definiera därför
int min = 10;och sätt på liknande sätt max till 20 (inuti main). Därefter skall programmet anropasumFor(min,max)och skriva ut resultatet med hjälp avSystem.out.println(), ungefär som i exemplet ovan. -
Testkör!
Att förstå: while, do-while
Java har också två andra loop-konstruktioner, while
och do-while. De ser ut så här:
while (condition) {
statements
}
do {
statements
} while (condition);
Skillnaden mellan konstruktionerna är att do-while alltid
genomför loopen minst en gång, eftersom villkoret inte testas förrän
efteråt.
Dessa loop-konstruktioner är i grunden enklare
än for-loopen, och kan passa bra när man har andra
typer av slutvillkor som inte direkt kopplas till en variabel som
räknas upp i varje steg. Exempel (en kö är en lista element där
man bara lägger till i slutet och bara plockar i början, som när
man står i kö):
while (!queue.isEmpty()) {
// ... take first element from queue ...
// ... do something with it ...
}Att göra: while, do-while
Eftersom konstruktionerna är så lika testar vi bara en av dem.
-
Skapa nu funktionen
sumWhile(...), som har samma parametrar och returvärden somsumFor()men istället använder enwhile-loop för att beräkna samma summa. -
Ändra
main()så den även anroparsumWhile()och skriver ut resultatet från båda anropen. Testkör programmet. Får du alltid samma summor?
Uppgift 1.3: Multiplikationstabell
Syfte
Syftet med denna uppgift är att arbeta vidare med kontrollstrukturer samt att testa att skapa en namngiven konstant för att göra koden mer lättförståelig.
Att förstå: Välja multiplikationstabell
Vi börjar med att skapa ett program som skriver ut multiplikationstabellen för ett "hårdkodat" (fixerat) tal, t.ex. 5.
Istället för att bara använda en konstant som 5 "rakt av" är det
dock oftast bättre att ge den ett symboliskt namn, t.ex. genom
att deklarera en konstant TABELL med värdet
5. Detta underlättar både kodförståelse ("TABELL" är lättare att
förstå än "5") och senare ändringar (lättare att ändra den enda
deklarationen än att ändra värdet "5" på massor av platser i
koden).
Att göra: Välja multiplikationstabell
Börja med att skapa klassen Exercise3 för uppgiften.
Deklarera en konstant som anger vilken multiplikationstabell vi skall skriva ut. Denna skall vara synlig endast i klassen och bör deklareras som följer, på toppnivå i klassen:
private final static int TABELL = 5;
Här stöter vi på Javas namngivningsstandard som säger att namn på denna
typ av konstanter skall skrivas med stora bokstäver. Att "variabeln"
är final gör att dess värde inte kan ändras, så att den
faktiskt blir en konstant. Att den är static gör att den
bara lagras en gång i klassen, istället för i varje objekt av
typ Exercise3 (om vi nu hade skapat några sådana objekt).
Djupare förklaringar av detta kommer under föreläsningarna.
Verktyg: Kodkomplettering och analys
När ni skriver kod i IDEA kommer ni att märka flera saker.
IDEA kommer att föreslå fortsättning på ord, något ni kan använda för att snabbt fylla i långa namn. Man väljer det alternativ som passar, t.ex. genom att skriva tills man lätt kan markera rätt namn och sedan trycka på TAB.
IDEA kommer också att föreslå och markera fel eller andra otydligheter i koden. Genom sin indexering vet IDEA alltid vad ett namn står för. På så vis kan den välja olika färgmarkeringar (syntax highlighting) för att indikera vad som är en klass, en statisk funktion mm. vilket underlättar läsning av kod.
Att förstå: Utskrift och strängkonkatenering
Nu är det dags att programmera iterationen och utskriften. I
Java sätts strängar för utskrift samman genom konkatenering via
operatorn '+'. När man försöker "addera" ett tal
och en sträng förstår Java automatiskt att talen ska konverteras
till strängar. Man kan därför göra en utskrift enligt följande
exempel, där i är en loopvariabel:
System.out.println(i + " * "+TABELL + " = " + ...); Att göra: Utskrift
-
Konstruera en loop som skriver ut den valda multiplikationstabellen: 1*TABELL, 2*TABELL, osv. upp till 12*TABELL.
-
Testkör programmet på samma sätt som i tidigare uppgift.
Uppgift 1.4: Inmatning
Syfte: Testa inmatning från användaren!
Syftet med denna uppgift är delvis att testa inmatning av värden från en användare, men även att utforska typer via konvertering från strängar till heltal.
Att förstå: Inmatning
Vi vill nu låta användaren ange vilken multiplikationstabell som ska visas. Vi gör detta genom en utökning i samma klass som tidigare.
I Java kan vi läsa in information från kommandofönstret med hjälp av klassen Console. Här väljer vi istället att läsa in ett värde från en grafisk dialogruta, vilket faktiskt är lika enkelt!
Att göra: Inmatning
-
Utöka programmet från förra uppgiften för att läsa in ett värde från användaren. Detta måste göras i mainmetoden, innan loopen. Exempel:
String input = JOptionPane.showInputDialog("Please input a value");IDEA kommer att markera att den inte känner till klassen
JOptionPane. Vi måste berätta var denna finns genom att antingen trycka Alt + Enter när IDEA föreslår detta, t.ex. då markören står framför raden, eller genom att trycka på den röda glödlampan som dyker upp efter en stund till vänster på raden och välja Import Class. -
Värdet som läses in är en sträng, och måste konverteras till ett heltal (om möjligt). Exempel:
int tabell = Integer.parseInt(input);Då detta är en lokal variabel namnges den inte med stor bokstav. Ändra därför från
TABELLtilltabelli den tidigare utskriften så att det nya värdet används. -
Provkör!
Testa gärna att mata in en icke-numerisk sträng och se vad som händer. Vi lämnar som överkurs (frivilligt) att ta hand om felet som uppstår och låta användaren försöka på nytt.
Uppgift 1.5: Felsökning med IDEAs hjälp
Syfte: Hitta syntaxfel
Denna uppgift syftar till att testa hur en programmeringsmiljö kan hjälpa till att hitta fel i koden.
Att förstå: Syntaxfärgläggning som ett verktyg
Det händer ofta när man skriver kod att något inte blir syntaktiskt korrekt. IDEA och många andra omgivningar hjälper till att lösa dessa problem innan man kompilerar genom syntaxfärgläggning och markering av fel och problem. Vi demonstrerar detta med hjälp av fakultetsfunktionen.
Att göra: Syntaxfärgläggning
-
Börja med att precis som ovan skapa klassen
Exercise4. I den, inuti klassdefinitionen (mellan måsvingarna{}), klistrar du in följande felaktiga kod:public static void main(String[] args) { for (int i = 0; i < 10; i+1) { system.out.println(i + "-fakultet: " + facrotial(i)); } } /** * Calculates f! given f. * @param f * @return f! */ private factorial(int f) { if (f = 0) return 1; } int result = 1 for (int i = 1; i <= f; i+1) { result *= i; } return result }IDEA kommer helt utan att kompilera koden att känna av och markera en hel del fel. Det finns ett 10-tal fel varav ett är att "
static"-kod i detta fall endast kan anropa annan "static"-kod. - Se till att koden blir körbar och skriver ut 0-fakultet till och med 10-fakultet.
-
Testa att skriva ut n-fakultet för större värden på n. Hur
långt kan man komma? Var börjar det bli fel? Varför? (Om du
inte vet svaret kommer vi att titta på det senare.)
Uppgift 1.6: Felsökning med debugger
Syfte: Börja testa debuggern
En debugger (avlusare) kan vara ett extremt användbart verktyg vid programmering. Syftet med denna uppgift är att introducera debuggern så tidigt som möjligt, för att förhoppningsvis spara mycket tid i senare skeden. Målet här är egentligen inte är att få ett fungerande program, utan att se hur man lagar ett trasigt program – därför får vi ta en del "omvägar"!
Att förstå: Primtalsletare, statiska metoder
För att även få lite mer programmeringsvana i Java skriver vi ett nytt program att avlusa. Detta program kommer att testa om ett tal är ett primtal.
När vi ska införa en väl avgränsad funktionalitet, som att testa primtal, bör den separeras ut för att förbättra modularitet och läsbarhet. Primtalstestet implementeras därför i en separat metod.
Att testa primtal är en sorts primitiv funktionalitet där man kan hävda
att objektorientering egentligen inte behövs. Med andra ord, vi vill inte
nödvändigtvis skapa ett objekt som är en primtalstestare, och
sedan fråga det objektet om ett visst tal är ett primtal. Istället kan
det kännas naturligt att använda en
ren funktion isPrime(), precis som i Pythonkursen.
Men Java har inga "rena" funktioner som existerar utanför klasser. Vad vi
har är statiska metoder som existerar i själva klassen utan att
vi först skapar objekt av klassen. Detta är något som ska användas
sparsamt men som faktiskt är lämpligt just för isPrime(). Vi
kommer att diskutera detta i mer detalj under en av föreläsningarna.
Att göra: Primtalsletare
-
Skapa en ny klass
Exercise5precis som tidigare. -
Skapa en egen metod,
public static boolean isPrime(int number), vars ansvar är att testa omnumberär ett primtal.I metoden lägger vi en
for-loop som går igenom alla tal 2,3,..., inparameter-1 och ser om någon delar talet. I så fall returneras false, annars true. Här behövs alltså enif-sats inuti for-loopen.För att avgöra om ett tal delar inparametern använder vi följande felaktiga kod:
int rest = number / i; if (rest == 0) { // number är en jämn multipel av i ... } -
Vi testkör nu funktionen. Låt
main()skriva ut resultatet avisPrime(5). Starta klassen som vanligt. Svaret bör blitrueom du har gjort rätt.Modifiera programmet så att
main()även skriver utisPrime(4). Det blir ocksåtruevilket ju är fel. Vi har alltså upptäckt ett fel i programmet.
Att förstå: Påbörja avlusning
Vi kunde nu lägga till utskrifter för att ta reda på vad som egentligen händer i programmet, men det finns ett mer flexibelt sätt: Vi använder debuggern och ser till att programmet automatiskt stannar för inspektion vid en specifik brytpunkt (breakpoint).
Att göra: Påbörja avlusning
-
Sätt en brytpunkt på raden
if (rest == 0)genom att vänsterklicka i listen till vänster om koden eller genom att stå på raden och trycka CTRL-F8. En brytpunkt indikeras genom en röd cirkel i listen till vänster samt genom att raden blir färgmarkerad. -
Starta programmet i debuggern genom att högerklicka och välja Debug Exercise5.main() (inte "Run"!). Det ger följande fönster:
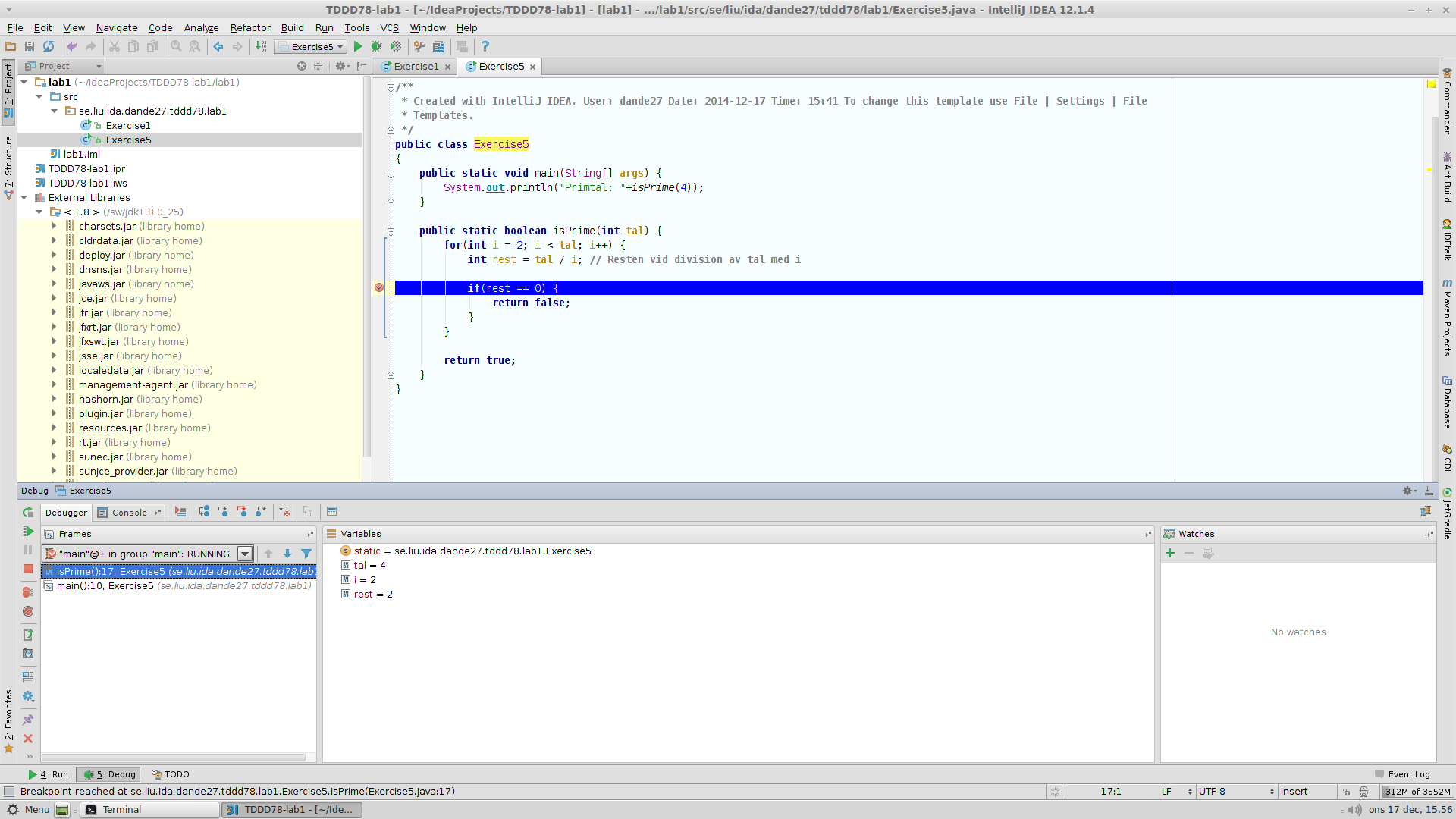
Programmet har nu startats, men har automatiskt pausats då brytpunken nåtts. Detta visas genom att raden med brytpunkten får blå färg.
Notera att debug-fönstret visas under kodfönstret. I debug-fönstret finns som standard tre mindre fönster. Det vänstra visar vilken anropskedja som ledde oss till funktionen vi befinner oss i körs – i det här fallet anropades den från
main(). Det mittersta visar intressanta variabler och deras värden. Det högra visar Watches som är variabler vi valt att hålla extra koll på (för närvarande inga). -
Nu är det dags att se vad som har hänt.
I debuggern ser vi att vi att
number=4 ochi=2. Vi ser i koden att vi försökte hitta resten vid division medi, och i debuggern att resten faktiskt blev 2, vilket inte är vad vi förväntat oss. 4 är ju jämnt delbart med 2!Alltså måste något vara fel på den tidigare raden och mycket riktigt, / borde ju vara en annan operator. Vilken? Ändra detta och testkör (starta om debuggern) för att se att 4 inte längre klassas som ett primtal.
-
När allt fungerar kan du avsluta debuggningen genom att trycka på den röda stoppknappen till vänster eller genom att trycka Ctrl-F2. Notera att debug-fönstret under koden stannar kvar. Du kan antingen stänga det eller växla tillbaka till run-fönstret.
Diskussion: Vad har vi uppnått?
Just i detta fallet ser man kanske inte omedelbart poängen. Men för mer komplicerade fel är debuggern enormt användbar, och under kursen kommer ni sannolikt att bekanta er mer med den.
En stor fördel är att ni omedelbart kan se värden på alla variabler. Ni kan också inspektera egenskaper hos objekt och följa pekare till andra objekt, till exempel gå in på detaljerna i varje objekt i en lista. Detta kommer ni att se mer av när vi kommer in på objektorientering.
Att debugga kod utan att ta hjälp av en debugger är möjligt, så kallad "print-debuggning" där man lägger in utskrifter av önskade variabler eller programflöden på strategiska ställen. Sedan kompilerar man och flyttar utskrifterna allt eftersom man får mer information om var man skall söka efter buggarna.
Med hjälp av debuggern kan man istället få ut all information direkt och behöver inte kompilera och köra om programmet många gånger för att lokalisera en bugg. Det är därför väldigt tidsbesparande och ger även en inblick i hur koden faktiskt exekverar vilket leder till ökad förståelse.
Man kan också skapa automatiska brytpunkter när undantag (exceptions) kastas, eller se till att programmet bara avbryts (pausas) om vissa villkor är uppfyllda. Det gör det mycket enklare att hitta fel som är oväntade eller som bara inträffar ibland. I den situationen är det speciellt värdefullt att kunna utforska hela programmets tillstånd, och alla variabler. Vid "print-debuggning" är risken att man lägger till några utskrifter, testar i flera timmar för att trigga felet, och sedan till slut upptäcker att man borde ha skrivit ut ytterligare en variabel...
Verktyg: Vad mer kan man göra i debuggern?
Run-menyn visar tillgängliga operationer att göra i debugläget. De vanligaste är:
- Step Over | F8 som exekverar en rad kod och går till nästa utan att gå in i funktionsanrop.
- Step Into | F7 som exekverar en rad kod och om raden innehåller ett funktionsanrop så hoppar den in i funktionen.
- Run to Cursor | Alt+F9 som exekverar tills den kommer till nuvarande markörposition. Detta är samma som att lägga till en brytpunkt, köra till den och sedan ta bort den igen, ett förfarande som ofta används.
- Run | F9 kör vidare till nästa brytpunkt.
Det finns många avancerade sätt att underlätta debuggning, t.ex. att köra tills ett givet villkor är sant, eller tills en given rad exekverats ett bestämt antal gånger. Ni kan hitta mer information via IDEAs hjälpsida.
Att göra: Hitta fler primtal
Vi avslutar den här uppgiften genom att skriva ut alla primtal under 100.
Gör en for-loop i main()
metoden. Iterera över talen från 2 till 100 och skriv ut alla
som klassificeras som primtal.
Det finns en fori-mall för att snabbt få till en
for-loop. Använd den på samma sätt som psvm
och sout.
Uppgift 1.7: Mer kontrollstrukturer
Syfte: Bli bekant med switch-konstruktionen
Vi ska nu titta på switch, som i vissa fall är ett
mer läsbart och koncist alternativ till if.
Att förstå: Switch
Vi ska nu testa en alternativ villkorssats: switch.
Denna villkorssats testar inte godtyckliga villkor. Istället
anger man ett uttryck, och vilken gren man utför beror enbart på
detta uttrycks värde. Detta kan bli mer läsbart då man
slipper upprepa uttrycket man vill jämföra.
Sedan Java 7 fungerar switch med heltal, enum-typer, och
strängar. Mest stöd från IDEA fås vid användning av enum-uttryck i
switch-satsen eftersom IDEA då känner till vilka möjliga grenar som finns.
Att göra: Switch
-
Vi skall utöka koden i uppgift 1.2. Låt
main()användaJOptionPane.showInputDialogför att läsa in en textsträng som skall vara "for" eller "while".Låt switch-satsen anropa rätt summeringsfunktion beroende på denna input. Glöm inte
break!Lägg även till en
default-etikett i switch-satsen. Denna gren utförs om man inte skrev in något av de acceptabla valen och bör alltså skriva ut ett felmeddelande. -
Testa programmet!
Uppgift 1.8: Kortslutning av logiska operationer
Syfte
I Java finns två olika sätt att utföra de logiska operationerna and och or. Det är viktigt att man känner till skillnaderna i hur de fungerar. Om man gör fel kan det leda till att onödiga eller potentiellt farliga beräkningar görs.
Att förstå: Kortslutning
I Python finns operatorerna and och or. Båda dessa
är kortslutande, vilket betyder att om resultatet är känt
efter att första operanden beräknats kommer den andra aldrig att
beräknas.
Konkret: Om Python behöver värdet av a and b börjar man med att räkna ut värdet på a. Om a är falskt vet man att a and b kommer att vara falskt oavsett vilket värde b råkar ha: Både false and false och false and true är ju falskt. Då struntar man helt enkelt i att beräkna b, för dess värde spelar ingen roll. På samma sätt fungerar a || b, men där slutar man beräkningarna om man har fått reda på att a är sant.
Samma funktionalitet finns i Java, med && istället för and och med || istället för or.
Men det finns också en variant av vardera operator där bara ett tecken används istället: a & b och a | b. I dessa uttryck garanteras att både a och b räknas ut. I vissa fall kan detta vara användbart, men som vi ska illustrera nedan är det oftast den kortslutande varianten man vill ha.
Att göra: Kortslutning
-
Skapa en ny klass, Exercise8, med en tom main-metod. Skriv sedan funktionen
askUsersom tar som inparameter en sträng som kommer att presenteras för användaren av programmet. Funktionen skall returnera sant om användaren svarar "ja", vilket åstadkoms genom att returnera det booleska värdet av följande uttryck:JOptionPane.showConfirmDialog(null, question, "", JOptionPane.YES_NO_OPTION) == JOptionPane.YES_OPTION -
Lägg till kod i main-metoden så att programmet ligger i en evig loop med hjälp t.ex. av en
while(true)-loop.Nu skall man få möjligheten att avbryta, men bara om man är helt säker. Detta görs genom att ställa frågorna
askUser("Quit?")ochaskUser("Really ?"). Om båda svaren frånaskUserblirtrueskall programmet avslutas (returnfrån main-metoden) och annars ska det skriva ut att programmet fortsätter köra.Prova båda varianter nedan (en i taget!) och ge olika svar på frågorna:
if (askUser("Quit?") && askUser("Really?")) { ... } if (askUser("Quit?") & askUser("Really?")) { ... }Vilken verkar bäst att använda i detta fall? Vad händer med respektive utan kortslutning?
Efter föreläsning 2, typer / allmän OO
Uppgift 1.9: Typning
Syfte
Typning i Java skiljer sig från hur det hanteras i Python. I Java sker typkontroll vid kompilering, eller i vårt fall ännu tidigare, så fort IDEA kan avgöra typerna.
Att göra
Vi skall återanvända ett exempel från Python-kursen, implementationen av Newton-Raphsons klassiska metod, i det här fallet hårdkodad för att hitta kvadratroten ur ett tal.
- Skapa en ny klass,
Exercise9, med en tommain-metod. Skriv sedan funktionenfindRootsom tar som inparameter endouble(vi vill ju räkna med decimaler) och returnerar endouble. -
Givet att inparametern heter
xskall funktionen först sätta variabelnguesstill detta värde och sedan utföraguess = guess - (guess*guess-x) / (2*guess);10 gånger innan den returnerar det slutliga värdet påguess. (Mer information om metoden finns här: Newton-Raphson.) - Lägg till inläsning av det värde vi vill hitta roten ur i main-metoden. Inläsning sker med hjälp av
JOptionPanepå samma sätt som tidigare:String x = JOptionPane.showInputDialog("Please input a value");Vad händer när du matar in koden? Går det att använda
xsom argument tillfindRoot? Hur kan IDEA annars veta att det inte går innan koden körs? -
Fixa koden genom att konvertera inmatningen till en double med hjälp av
Double.parseDouble. -
Se till att koden skriver ut resultatet, och testkör!
Att förstå: Automatisk typkontroll
Vi såg att när man använder IDEA kan typfel upptäckas direkt, utan att man ens behöver kompilera koden. IDEA indexerar fortlöpande koden i bakgrunden så att den kan hålla koll på alla variablers typer och alla funktionparametrar. På så vis kan många fel förhindras innan kompilering. Det gör även att IDEA kan hjälpa till att föreslå lösningar.
Som jämförelse kan sägas att Python normalt inte upptäcker liknande skrivfel förrän just den raden som innehåller felet körs. Moderna utvecklingsmiljöer som PyCharm kan göra en partiell typkontroll, men de kan ändå missa många problem av den här typen.
Att göra: Komplettering och typning
Det här är ett bra tillfälle att illustrera hur IDEAs funktion för komplettering blir mer kraftfull med hjälp av variabeltyper.
Testa i koden för uppgift 1.9 att ta bort parametern som skickas
till findRoot, och ställ sedan markören i den tomma
parentesen precis som om du höll på att skriva den här koden just nu:
System.out.println("Roten ur " + x + " är " + findRoot([markör]));
När du trycker Ctrl-space (basic code completion)
föreslår IDEA allt som skulle kunna stå i den här positionen.
Bläddra gärna i listan och se vad som är möjligt att skriva
här. Ett exempel är x, vilket kanske verkar
underligt eftersom x är en sträng – men man
hade kunnat använda till exempel x.length(),
vilket börjar med x.
Men nu vet du kanske att du vill använda dig av en variabel som redan är av rätt typ. Då trycker du Ctrl-shift-space (type completion). IDEA föreslår då endast att man kompletterar med något som direkt matchar typen på den valda positionen. I detta fall minskas möjligheterna avsevärt. Du kan läsa mer här: auto completion.
Uppgift 1.10: Primitiva numeriska datatyper
Syfte
Vi skall nu titta lite mer på skillnader mellan de olika datatyper som
används vid numeriska beräkningar. De vanligaste
är int, long, float och
double.
Att förstå: Olika numeriska datatyper
Det är viktigt att känna till skillnaden mellan olika primitiva datatyper. Speciellt kan man ibland välja fel datatyp för numeriska beräkningar.
I Python 3 finns en enda datatyp för heltal: int. Den
skiljer sig från heltal i de flesta andra språk genom att den själv utökar
sitt lagringsutrymme så att den kan lagra godtyckligt stora tal:
>>> 2 ** 1000
10715086071862673209484250490600018105614048117055336074437503883703510511249361224931983788156958581275946729175531468251871452856923140435984577574698574803934567774824230985421074605062371141877954182153046474983581941267398767559165543946077062914571196477686542167660429831652624386837205668069376
>>> 2 ** 10000
19950631168807583848837421626835850838234968318861924548520089498529438830221946631919961684036194597899331129423209124271556491349413781117593785932096323957855730046793794526765246551266059895520550086918193311542508608460618104685509074866089624888090489894838009253941633257850621568309473902556912388065225096643874441046759871626985453222868538161694315775629640762836880760732228535091641476183956381458969463899410840960536267821064621427333394036525565649530603142680234969400335934316651459297773279665775606172582031407994198179607378245683762280037302885487251900834464581454650557929601414833921615734588139257095379769119277800826957735674444123062018757836325502728323789270710373802866393031428133241401624195671690574061419654342324638801248856147305207431992259611796250130992860241708340807605932320161268492288496255841312844061536738951487114256315111089745514203313820202931640957596464756010405845841566072044962867016515061920631004186422275908670900574606417856951911456055068251250406007519842261898059237118054444788072906395242548339221982707404473162376760846613033778706039803413197133493654622700563169937455508241780972810983291314403571877524768509857276937926433221599399876886660808368837838027643282775172273657572744784112294389733810861607423253291974813120197604178281965697475898164531258434135959862784130128185406283476649088690521047580882615823961985770122407044330583075869039319604603404973156583208672105913300903752823415539745394397715257455290510212310947321610753474825740775273986348298498340756937955646638621874569499279016572103701364433135817214311791398222983845847334440270964182851005072927748364550578634501100852987812389473928699540834346158807043959118985815145779177143619698728131459483783202081474982171858011389071228250905826817436220577475921417653715687725614904582904992461028630081535583308130101987675856234343538955409175623400844887526162643568648833519463720377293240094456246923254350400678027273837755376406726898636241037491410966718557050759098100246789880178271925953381282421954028302759408448955014676668389697996886241636313376393903373455801407636741877711055384225739499110186468219696581651485130494222369947714763069155468217682876200362777257723781365331611196811280792669481887201298643660768551639860534602297871557517947385246369446923087894265948217008051120322365496288169035739121368338393591756418733850510970271613915439590991598154654417336311656936031122249937969999226781732358023111862644575299135758175008199839236284615249881088960232244362173771618086357015468484058622329792853875623486556440536962622018963571028812361567512543338303270029097668650568557157505516727518899194129711337690149916181315171544007728650573189557450920330185304847113818315407324053319038462084036421763703911550639789000742853672196280903477974533320468368795868580237952218629120080742819551317948157624448298518461509704888027274721574688131594750409732115080498190455803416826949787141316063210686391511681774304792596709376
I de flesta språk har man istället fixerad storlek på heltalstyperna.
Java har bland annat de primitiva typerna int (32 bitar)
och long (64) bitar. Då är det viktigt att förstå vad som
kan hända om en beräkning överskrider kapaciteten hos variabeln.
BigInteger, men detta kräver en helt annan syntax.
När det gäller flyttal är det inte lika enkelt att ha godtycklig "storlek", bland annat för att många beräkningar (som 1/3) inte alls kan representeras med ett ändligt antal decimaler. Där har även Pythons "vanliga" flyttal ändlig precision – i de flesta implementationer används 64-bitars flyttal.
Java erbjuder istället två typer: double, som alltid har 64
bitar, och float, som har 32 bitar. Här använder man
normalt double, men float kan t.ex. användas då
man lagrar många flyttal och vill spara minne.
Eftersom datatyperna i Java har begränsade storlekar finns det gränser för vad som kan representeras av de olika typerna.
Att göra: Olika numeriska datatyper
Skapa en ny klass,
Exercise10, med en tommain-metod. Vi skall nu lägga till kod tillmain-metoden.-
Börja med att lägga till
int tal = 16777216;. Vi skall nu konvertera denna till enfloatoch sedan tillbaka tillintför att se vad som händer. Lägg därför tillfloat decimaltal = tal;. Lägg märke till att eftersom det talområde som kan representeras av enfloatär större än motsvarande för enintaccepteras detta av Java. Det sker en implicit typkonvertering, dvs vi behöver inte skriva något extra. -
Konvertera nu tillbaka genom att lägga till
int tillbaka = decimaltal;. Vad händer?I det här fallet kan inte decimalerna för en
floatrymmas i enintoch Java kräver att man hanterar detta, t.ex. genom att göra en explicit typkonvertering (avrundning) genom att skrivaint tillbaka = (int)decimaltal;. Då visar man att man verkligen ville bli av med decimalerna. -
Skriv ut
tal,decimaltalochtillbakaoch jämför vilka värden som skrivs ut. Ändra sedan från 16777216 till 16777217 och jämför utskrifterna. Vad händer? -
Byt typ på
decimaltaltilldoubleoch jämför resultatet. Vad händer? -
Lägg till nya variabler
int big = 2147483647;samtint bigger = big+1. Gissa först vad som kommer att skrivas ut och skriv sedan ut värdena. Blev det som ni tänkt? Byt datatyp påbiggertill en större,long, och jämför. Vad hände? -
Testa att ändra
biggers definition tilllong bigger = big+1L;och notera resultatet. Slutligen ändrar vi tilllong bigger = (long)big+1;och jämför.
Att förstå: Primitiva numeriska datatyper
Vi skall nu förklara vad vi sett.
Till att börja med sker konvertering implicit om den mottagande typen
innehåller talområdet för den föregående typen, dvs från int
och long sker implicit konvertering till float
och double. På andra hållet krävs explicit konvertering
eftersom det inte är säkert att den mottagande typen kan representera
värdet.
Vad som inte skyddas mot är att man förlorar information vid konvertering
mellan heltal och flyttalstyper. Vi såg exempel på det när 16777216 och
16777217 representerades av samma float. Detta beror på att flyttal kan
representera ett större talområde, men innehåller bara samma mängd
information som motsvarande heltal (int och float består av 32 bitar data
medan long och double består av 64 bitar data). När vi bytte från float till
double gick det däremot bra att behålla informationen om
heltalet 16777217 eftersom det finns mer plats i en double
vilken därför har noggrannare precision i de tal den representerar.
Vi får liknande problem när vi avrundar från float
till int då t.ex. (int)Math.PI blir 3. Även har
tappas information, men detta är dock något vi är mer vana vid och därför
mer sällan gör fel på.
I steg 6-7 undersökte vi relationen mellan int och long. Vi såg att om vi
försöker representera ett tal större än vad som ryms i en int så slår talet
runt och blir negativt. Detta är uppenbart något man behöver hålla koll
på. Med hjälp av en long kan man minska risken att detta händer då mycket
större tal kan representeras.
Vi såg att det inte sker någon automatisk konvertering
från int till long när talet blir för stort för
en int. I vårt fall (long bigger = big+1) är det
så att både big och 1 är av typen int vilket
innebär att resultatet av additionen blir en int. När detta
sedan tilldelas till en variabel av typ long är skadan redan
skedd. För att få additionen att ske i storleken long måste
minst en av de båda ingående talen vara en long. Om det är
olika storlek/precision på de ingående talen kommer det mindre att
konverteras till den större typen och resultatet vara av den större typen.
I vårt fall uppnås detta genom att vi antingen deklarera konstanten 1 som
en long (1L) eller genom att explicit
konvertera big till long.
Tetris 1.11: Introduktion till Tetris
Syfte
Utöver att titta på enskilda delar av Java och OO kommer labbserien också att ge dig möjlighet att skriva ett fullständigt program. Där kommer du också att få utforska olika OO-begrepp och modelleringsfrågor, och du kommer att testa enklare GUI-programmering i Java.
Det program vi har valt är ett enklare Tetris-spel. En fördel med Tetris som spel är att det inte är så krävande i fråga om t.ex. animering, kollisionsdetektering och andra knepigheter, så att vi kan fokusera mer på programmering och hur man kan tänka för att skriva ett objektorienterat program.
Ämnen som kommer att ingå i Tetris-delen av labbserien är bland annat följande. Som du ser motiveras alla ämnen både av behov i spelet och av det man behöver lära sig i kursen!
- Modellera enskilda objekt:
- Spelbräde – enklare objektorienterad modellering
- "Brickor" med form och färg – mer objektorienterad modellering
- "Visare" för spelbräde – uppdelning av ansvarsområden
- Modellera sammanhang:
- Hur vet "visaren" när något har ändrat sig? – hur man kan tänka på dataflöde i ett program
- Visualisering och GUI:
- Enkelt, med text – att börja enkelt för att kunna testa koden tidigt
- Grafiskt – "rita" block att börja enkel GUI-programmering
- Menyer, tangentbordshantering, ... – begrepp i händelsehantering (events) med mera
- Spelmekanik:
- "Driva" spelet med en timer – en introduktion till tidsstyrd programmering
- Hantera spelets regler – en hel del "ren programmering"
- Highscorelista – mer OO-modellering
- Rotation av brickor, ... – implementera algoritmer i Java
- Powerups – hur programmerar man modulärt?
Detta varvas med uppgifter utanför Tetris, när vi behöver titta på t.ex. vissa modelleringsfrågor som inte passar in lika bra i Tetris.
För att leda dig åt rätt håll när du omsätter teori till praktik är de första delarna i Tetris i "tutorial"-form, där vi ganska detaljerat diskuterar hur man kan tänka för att överföra idéerna till kod. Mot slutet av labbserien får du gradvis mer och mer frihet – och färre detaljerade ledtrådar.
Det mesta av programmeringen kommer att ske i labb 2 och 3, efter att du har lärt dig om objektorientering, men redan nu kan vi börja med några förberedelser.
Att göra: Prova Tetris
Läs gärna på lite om Tetris. Det kan hjälpa dig i resten av labbserien.
-
Om du inte har spelat Tetris tidigare: Testa någon gratisvariant, t.ex.
M-x tetris RETi vissa varianter av Emacs. Uppgifterna kommer att förutsätta att du vet hur Tetris fungerar.
Att förstå: Bryta ner i steg, milstolpar
Hur programmerar man ett lite större sammanhängande projekt såsom ett Tetris-spel? Ett tips är att bryta ner det i steg eller milstolpar som kan implementeras i tur och ordning – helst på ett sätt som gör att man kan testa varje steg för sig och känna att man faktiskt har åstadkommit något. Instruktionerna för Tetris är uppbyggda på detta sätt, speciellt efter de första inledande stegen.
Tetris 1.12: Börja programmera Tetris
Syfte: Börja så smått med spelplanen!
Om vi ska implementera Tetris behöver vi bland annat ett sätt att representera spelets nuvarande tillstånd, t.ex. spelplanen. Vissa aspekter behöver vi lämna till labb 2, eftersom de kräver mer kunskaper om objektorientering, men vi kan i alla fall börja med:
Att diskutera hur spelplanen ser ut och hur delar av den kan modelleras.
Att skapa vår första egna datatyp, för "kvadrater" (detta kommer att förklaras snart).
Vi vill speciellt fokusera på hur man tänker när man modellerar. Därför går vi genom steg för steg hur vi har tänkt för att komma fram till de föreslagna datatyperna.
Att förstå: Skapa paket
Vi kommer att fortsätta i samma Git-arkiv och samma IDEA-projekt som du använder för alla labbar. Vi vill däremot separera Tetris från övriga klasser genom att lägga dem i olika (under)paket.
Att göra: Skapa projekt och paket
Skapa ett paket för Tetris, med lämpligt namn -- t.ex.
se.liu.ida.dinadress.tddd78.tetris.Paketnamnet måste innehålla "tetris" någonstans! Namnet kommer att användas av mjukvara som automatiskt separerar Tetris-kod från annan kod vid inlämning.
Att förstå: Tetris-begrepp!
Som vi vet efter förra uppgiften har Tetris en spelplan där tetrisblock steg för steg "ramlar ner" uppifrån. Varje block består av exakt fyra sammanhängande kvadrater i en viss färg och ett visst mönster – själva namnet Tetris kommer faktiskt från tetra (4).
Totalt 7 olika blockmönster är möjliga, bortsett från möjligheten att
rotera dem. Nedan syns en illustration från Wikipedia. Standardnamnen på
dessa block
är I, J, L, O, S, T
och Z.
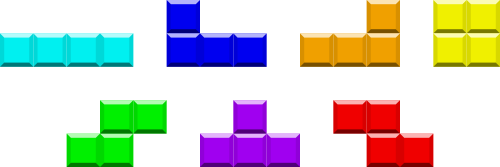
Så vad kallas egentligen den här typen av block, mer generellt? Man kan se dem som en variant av domino, som har 2 sammanhängande kvadrater:
Om vi då generaliserar från domino ("di-omino", di=2) får vi namnet polyomino, med specialfallen monomino (1), domino (2), tromino (3), tetromino (4), pentomino (5), hexonimo (6), och så vidare.
Varje tetrisblock är alltså en tetromino.
Att förstå: Modellering av kvadrater
Nu ska vi börja tänka genom alternativ för modellering. Läs genom hela rutan innan du börjar genomföra detta. Vi påminner om att vi vill diskutera hur vi tänker, inte bara slutresultatet!
Vi vill på något sätt representera den nuvarande spelplanen, det nuvarande läget i spelet. När man har spelat ett tag kan det till exempel se ut så här:

Men hur ska vi alltså representera detta tillstånd i ett program?
Vi kunde tänka oss att lagra en lista av de hela tetrisblock som
har ramlat ner samt x- och y-positioner för dessa block på planen. Men när
ett tetrisblock väl har "fallit på plats" kan ju vissa av dess kvadrater
så småningom försvinna medan andra finns kvar (att fulla rader försvinner
är ju själva poängen med spelet). Ovan ser vi t.ex. ett "helt"
grönt L men även 6
partiella L där vissa av
kvadraterna från det ursprungliga mönstret är borta. Detta vore det rätt
krångligt att representera med en lista över tetrisblock eftersom vi
skulle behöva hålla reda på vilka delar av varje tetrisblock som
fortfarande finns kvar.
Istället kan vi modellera på följande sätt: För varje position
(x,y) på spelplanen, är den tom? Och om inte, vilken typ
av tetromino tillhör kvadraten på den positionen? Varje gång ett block
faller på plats läggs det då in information om fyra nya kvadrater på
lämpliga (x,y)-koordinater. Vi behöver inte hålla reda på
vilket tetrisblock varje enskild kvadrat kom från. Vi behöver bara något
som indikerar vilken typ av kvadrat vi har på en viss position:
Kommer kvadraten ursprungligen från ett L,
ett J, ...? Det behöver vi så att vi senare vet vilken färg
som ska ritas ut.
Hur representerar vi då en "typ av kvadrat"? Vi vill kunna
representera exakt 8 olika värden: "här finns ingen kvadrat", "här
finns en kvadrat från ett I-block", "här finns en kvadrat från ett
T-block", och så vidare.
Java stödjer enum-typer, som är gjorda just för situationen när en datatyp har ett fast antal värden. "Enum" kommer från "enumeration", dvs. "uppräkning". Vi vill räkna upp de 8 värden som finns, och sedan ska man inte kunna skapa nya.
Enum-typer är egentligen klasser, och typens värden är objekt, men det behöver vi egentligen inte tänka så mycket på just nu.
Vi ska därför skapa en enum-typ med namn SquareType.
Att göra: Kvadrater
Skapa en enum-typ genom att högerklicka på Tetris-paketet i IDEA, välja New | Java Class och sätta "Kind" till Enum. Ge klassen namnet
SquareType.Lägg in följande inom klamrarna:
EMPTY, I, O, T, S, Z, J, LKlassen ser alltså ut så här:
public enum SquareType { EMPTY, I, O, T, S, Z, J, L }Detta betyder helt enkelt att typen
SquareTypehar värdenaSquareType.EMPTY,SquareType.I,SquareType.O, och så vidare. Eventuellt klagar IDEA på att namnen är för korta. Detta kan du ignorera.Här finns mer information om enum-typer om du skulle vara nyfiken på mera detaljer.
Avslutning
Här slutar första laborationen. Visa slutresultatet för din handledare och passa på att fråga om det är något du undrar över. Du behöver inte lämna in din kod just nu, men det du har skrivit kommer att följa med i inlämningen i labb 3, och kommer att vara en del av din slutliga implementation av Tetris.
Du kan också fortsätta direkt med nästa labb om handledaren är upptagen (se tidplanen för demo-deadlines), men ta ändå chansen att få återkoppling på vad du har gjort hittills!
Labb av Jonas Kvarnström, Mikael Nilsson 2014–2019.
Sidansvarig: Jonas Kvarnström
Senast uppdaterad: 2019-02-05

