Algoritmer

Introduktion

Under kursens gång har ni själva implementerat ett antal algoritmer. En algoritm är ju helt enkelt en tydlig specifikation för hur ett problem eller en klass av problem ska lösas, där algoritmen för att skriva ut en multiplikationstabell (i labb 1) kan beskrivas så här i pseudokod:

Låt n vara ett heltal som användaren matar in
För alla k från 1 till 12
    Skriv ut n * k

För vissa vanliga problem finns det många olika vedertagna algoritmer, som löser problemen på olika sätt. Varje algoritm (lösningsmetod) har då sina fördelar och nackdelar jämfört med de andra. I detta avsnitt ska vi ta en titt på ett antal sådana vedertagna algoritmer, framförallt för sortering av värden.

Sorteringsproblemet

Det gemensamma problem som sorteringsalgoritmerna löser är sorteringsproblemet. Vi kan konkretisera det genom att anta att vi har en (ändlig) hög med kort som vardera har ett heltal på framsidan. Högen är blandad och vår uppgift är att sortera den i stigande ordning.

Det finns flera många sätt att göra det på, som enbart baserar sig på att vi kan jämföra kortens värden (vilket är mindre / ska vara före?) och byta plats på korten.

Selection sort

Informell beskrivning

Selection sort gör följande med en osorterad hög (lista):

Skapa en ny hög med 0 kort. Denna hög är nu sorterad (inget är i o-ordning).
Gå igenom den osorterade högen och hitta kortet med det minsta talet.
Flytta detta kort till slutet av den sorterade högen. Denna hög måste fortfarande vara sorterad. Annars skulle ju det nya kortet vara mindre än något kort som redan fanns i den sorterade högen, men då skulle det kortet ha flyttats över tidigare, så detta kan inte hända.
Upprepa steg 2 och 3 till den osorterade högen är tom.

Alternativt kan man implementera selection sort utan en separat hög, genom att flytta kort inom den ursprungliga högen (till exempel för att spara minne). Detta illustreras av figurerna nedan.

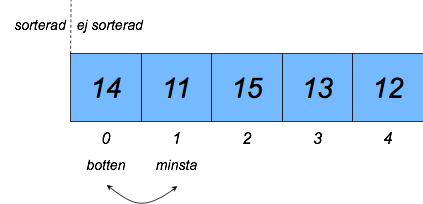
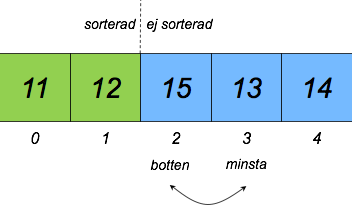
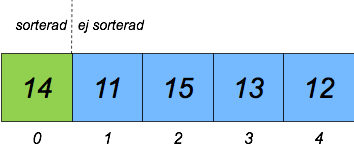
Gå igenom den osorterade delen av högen (positionerna 1-4 i andra bilden nedan) och hitta kortet med det minsta talet (exempelvis 12 i andra bilden nedan).
Byt plats på det upphittade kortet och kortet i "botten" av den osorterade delen (position 1 med kortet 14 i andra bilden nedan).
Upprepa steg 1 och 2 till ingen del av högen är osorterad.

Illustration

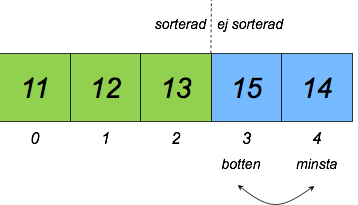
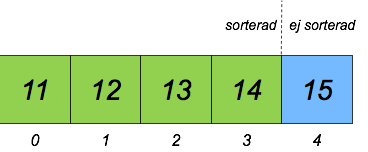
Den andra varianten av selection sort kan illustreras så här:

Du får gärna titta vidare på hur denna sortering fungerar:

http://www.sorting-algorithms.com/ visar flera sorteringsalgoritmer. Notera att detta inte visar vad som är snabbast: Eftersom animeringarna är gjorda för att illustrera de viktigaste stegen har de olika grad av "nedsaktning".
Selection-sort-dansen

Implementation

Som vi såg kan selection sort implementeras på två olika sätt. Följande implementation är kanske enklast att förstå och motsvarar den första pseudokoden ovan. Implementationen är destruktiv och förstår originallistan fullständigt: Den blir tom efter att funktionen anropas, eftersom alla element har förts över till den nya resultatlistan.

def selection_sort_copy(seq):
    """ Sorts a list using selection sort. """
    res = []
    while seq:
        e = min(seq)
        res.append(e)
        seq.remove(e)
    return res

Den andra implementationen är endast destruktiv i den mening att elementen i den ursprungliga osorterade listan flyttas om, så att listan blir sorterad.

def selection_sort_inplace(seq):
    """ Sorts a list using selection sort. """
    n = len(seq)
    for bottom in range(n-1):
    	# Osorterade delen börjar på position bottom
        # Hitta position för minsta elementet i osorterade delen
        minpos = bottom
        for i in range(bottom+1, n):
            if seq[i] < seq[minpos]:
                minpos = i
	# OK, vi vet var minsta elementet är
	# Byt plats på detta och "botten"
        seq[bottom], seq[minpos] = seq[minpos], seq[bottom]

Insertion sort

Informell beskrivning

Insertion sort gör följande:

Dela upp högen i två delar: en del som innehåller det första kortet (som vi anser är en sorterad hög) och en del som innehåller resten.
Ta det översta kortet i resten och sortera in det på rätt plats i den sorterade högen.
Upprepa steg 1 och 2 till dess att vi gått igenom alla kort

Skillnaden mot selection sort är alltså:

Det är lättare att hitta vilket kort man ska ta ur den osorterade delen av högen: Man tar helt enkelt det första, utan att leta efter det minsta.
Men sedan måste man göra mer arbete för att placera in det i den sorterade delen. Istället för att kunna placera det valda kortet sist, måste man leta efter var man kan stoppa in det.

Illustration

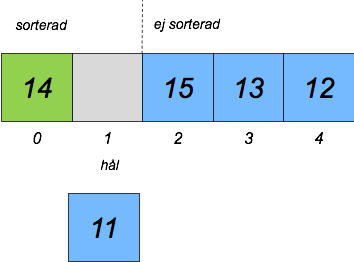
Efter steg 1:

Vi plockar det första elementet i osorterade delen:

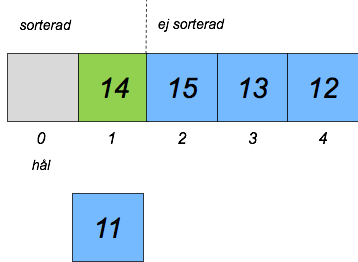
Vi flyttar om elementen i sorterade delen så att hålet ligger på rätt plats:

Vi stoppar in elementet där:

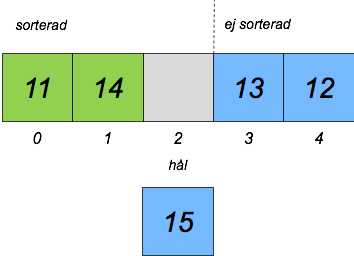
Vi plockar återigen det första elementet i osorterade delen:

Vi flyttar om elementen i sorterade delen så att hålet ligger på rätt plats (vilket det redan gör!) och stoppar in det valda elementet där:

Du får gärna titta vidare på hur denna sortering fungerar:

http://www.sorting-algorithms.com/ visar flera sorteringsalgoritmer. Notera att detta inte visar vad som är snabbast: Eftersom animeringarna är gjorda för att illustrera de viktigaste stegen har de olika grad av "nedsaktning".
Insertion-sort-dansen

Implementation

Precis som med selection sort så kan detta göras på två sätt; antingen så sorterar vi i samma lista som vi fick in (inplace), eller så skapar vi en ny resultatlista (copy).

def insertion_sort_copy(seq):
    """ Sorts a list using insertion sort. """
    res = []
    for e in seq:
        # Enkelt att välja ett element ur osorterade listan,
	# men nu måste vi se var i nya listan vi ska stoppa in det
        i = 0
        while i < len(res) and res[i] < e:
            i += 1
	# Stoppa in!  Här finns faktiskt inget hål,
	# utan insert() flyttar elementen för att skapa ett.
        res.insert(i, e)
    return res

def insertion_sort_inplace(seq):
    """ Sorts a list using insertion sort. """
    # Börja på 1 eftersom element 0 redan anses sorterat
    for i in range(1, len(seq)):
        # Plocka elementet från position i
        item = seq[i]
	# Nu är hålet där
        hole = i
	# Flytta hålet till vänster, ett steg i taget
        while hole > 0 and seq[hole-1] > item:
	    # Exempel: Se början av illustrationen.
	    # Där hade vi hole=1, item=11, seq[hole-1]=14, 14 &gt; 11.
	    # Hålet fanns först efter värdet 14,
	    # men flyttades sedan så det var före värdet 14.
            seq[hole] = seq[hole-1]
            hole -= 1
        seq[hole] = item

Rekursiva algoritmer

Som ni kanske har märkt tidigare så kan en rekursiv implementation ofta vara kortare och mer "elegant" än den iterativa. Men det finns också problem som lämpar sig särskilt bra att lösa rekursivt. Givet ett problem försöker man först lösa ett mindre problem (reskursivt) för att sedan utöka denna lösning till att gälla hela problemet. Denna metod kan ge upphov till mycket effektiva algoritmer.

Som första illustrerande exempel ska vi skapa en funktion anagrams som givet en sträng producerar en lista med alla anagram, det vill säga alla strängar som innehåller samma bokstäver i alla möjliga ordningar.

>>> anagrams('ab')
['ab', 'ba']
>>> anagrams('abc')
['abc', 'bac', 'bca', 'acb', 'cab', 'cba']
>>> anagrams('abcd')
['abcd', 'bacd', 'bcad', 'bcda', 'acbd', 'cabd', 'cbad', 'cbda', 'acdb', 'cadb', 'cdab', 'cdba', 'abdc', 'badc', 'bdac', 'bdca', 'adbc', 'dabc', 'dbac', 'dbca', 'adcb', 'dacb', 'dcab', 'dcba']

Induktiv metod

Hur kan vi tänka rekursivt när vi skapar just anagrams? Jo, om vi vill veta alla anagram för 'abc' kan vi basera detta på alla anagram för 'ab':

Anagrammen för 'ab' är ['ab', 'ba']. Detta är alltså alla (två) möjliga ordningar för bokstäverna a och b.
Om vi nu även har 'c' med i strängen, kan vi ta varje anagram för 'ab' och stoppa in 'c' på varje tänkbar position (först, i mitten eller sist):
- 'ab' => 'cab', 'acb', 'abc'
- 'ba' => 'cba', 'bca', 'bac'

Samma gäller för längre strängar. Man får de 24 anagrammen för 'abcd' genom att stoppa in 'd' på alla 4 möjliga positioner i de 6 anagrammen för 'abc'.

I figuren nedan gör man så, utom att man delar upp i 'a' och 'bc' istället för 'ab' och 'c'.

Anagramproblemets lösning

def anagrams(s):
    """ Creates a list with all possible anagrams of s """
    if s == "":
        # Tomma strängen kan bara ordnas på ett sätt: Tomma strängen
        return [s]
    else:
        ans = []
	first = s[0]
	rest = s[1:]
	# För varje anagram för resten av strängen
        for w in anagrams(rest):
	    # För varje position där man kan stoppa in första bokstaven
            for pos in range(len(w)+1):
	    	# Skapa ett nytt anagram
                ans.append(w[:pos] + first + w[pos:])
        return ans

Tornet i Hanoi

Tornet i Hanoi är ett klassiskt problem inom datavetenskap. Spelet går ut på att flytta samtliga skivor från den första pinnen till den sista utifrån några regler för förflyttning.

Endast en skiva i taget får flyttas
Skivorna får inte läggas åt sidan utan måste placeras på en av de tre pinnarna
En större skiva får aldrig placeras ovanpå en mindre skiva

Tänk nu att vi vill flytta alla skivor från vänstra pinnen till högra pinnen i bilden ovan. Vi måste så klart börja med att flytta den allra minsta skivan, men var kan vi placera den? Lägger vi den på högra pinnen kan vi inte stapla något på den (den är ju minst). I så fall måste den näst minsta skivan läggas på mittenpinnen. Men hur går man vidare? Är det rätt väg framåt?

Detta är som sagt ett välkänt problem och det finns en välkänd strategi för att alltid göra rätt. Vi börjar att visa hur man kan göra för några små exempel.

Flytta torn med 1 skiva från A till C:

Flytta 1 skiva från A till C

Flytta ett torn med 2 skivor från A till C med B som mellanlagring:

Flytta 1 skiva från A till B # Den minsta måste flyttas ur vägen
Flytta 1 skiva från A till C # Den större kommer på rätt plats
Flytta 1 skiva från B till C # Den minsta flyttas vidare till rätt plats

Fast detta är ju faktiskt samma sak som följande, som ser lite rekursivt ut:

Flytta ett torn med 2 skivor från A till C med B som mellanlagring:

Flytta ett torn med 1 skiva från A till B med C som mellanlagring
Flytta ett torn med 1 skiva från A till C med B som mellanlagring
Flytta ett torn med 1 skiva från B till C med A som mellanlagring

Och då kan vi gå vidare och hantera fler skivor:

Flytta ett torn med 3 skivor från A till C med B som mellanlagring:

Flytta ett torn med 2 skivor från A till B med C som mellanlagring # Ur vägen!
Flytta ett torn med 1 skiva från A till C # Största skivan från A till rätt plats!
Flytta ett torn med 2 skivor från B till C med A som mellanlagring # OK, er tur

Implementation

Utifrån detta kan vi se ett mönster. Mer generellt gäller:

Flytta ett torn med n skivor från x till z med y som mellanlagring:

Om n = 1
1. Basfall: Flytta skivan från x till z
Om n > 1
1. Flytta ett torn med n -1 skivor från x till y med z som mellanlagring
2. Flytta ett torn med 1 skiva från x till z med y som mellanlagring
3. Flytta ett torn med n -1 skivor från y till z som mellanlagring

def move_tower(n, source, dest, temp):
    """
    Print the instructions for moving n disks from source to dest
    using temp as interim storage.
    """
    if n == 1:
        print("Move disk from", source, "to", dest+".")
    else:
        move_tower(n-1, source=source, dest=temp, temp=dest)
        move_tower(1, source=source, dest=dest, temp=temp)
        move_tower(n-1, source=temp, dest=dest, temp=source)

Lite om komplexitet

Algoritmen är mycket kort, men varje anrop för n skivor ger upphov till *två rekursiva anrop med n - 1 skivor. Detta innebär att ett problem med n diskar kommer att kräva 2^n -1 antal steg, det vill säga problemet löses i exponentiell tid. Ett problem med 64 skivor kräver inte mindre än 18446744073709551615 steg för att lösas.

Antal skivor	Antal lösningssteg
1	1
2	3
3	7
4	15
5	31
6	63
7	127
8	255
9	511
10	1023

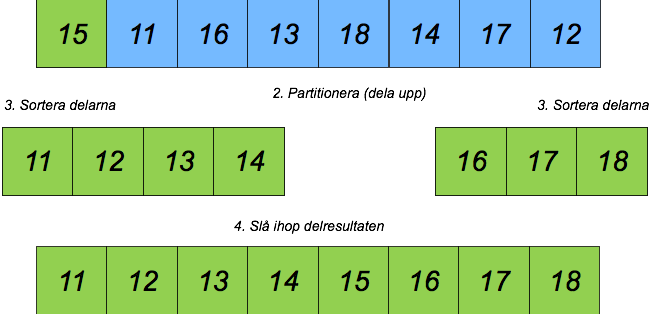
Quicksort

Vi återvänder nu till sortering för att se en algoritm som också bygger på att rekursivt lösa mindre delproblem och sedan kombinera lösningarna.

Informell beskrivning

Antag återigen att vi har en hög med kort som vardera har ett heltal på framsidan. Högen är blandad och vår uppgift är att sortera dem i stigande ordning. Detta kan vi göra så här:

Välj ut ett kort som vi kallar pivotelement
Dela upp resten av högen i två delar: en som innehåller alla kort som är mindre än pivotelementet och en som innehåller alla som är större än eller lika med pivotelementet
Sortera varje hög för sig genom att köra algoritmen från början
Lägg ihop de sorterade högarna i rätt ordning med pivotelementet i mitten

Men vad är basfallet då? Jo, vi delar bara högen i två delar om den har minst 2 element. Annars, med 0 eller 1 element, är högen redan sorterad. (I verkligheten finns några fler klurigheter, som fallet när alla element i högen har samma värde, och frågan om hur man väljer pivotelementet.)

Binära Träd

Inom datavetenskap används ofta trädstrukturer för lagring av och sökning i data. Ett binärt träd är en specialisering av generella träd där varje nod har 0, 1 eller 2 subträd, och där man dessutom håller reda på om ett enskilt barn är till vänster eller till höger. Man kan alltså ha ett "barn till höger" (barn nummer två) utan att ha ett "barn till vänster" (barn nummer ett)!

Binära sökträd (BST)

Binära sökträd är en ytterligare specialisering av binära träd, ett BST har följande egenskaper:

Binärt, d.v.s. varje nod har maximalt två grenar under sig.
Ordnade så att nyckeln i en viss nod är större än alla nycklar i vänstra grenen, och mindre än eller lika med alla nycklar i högra grenen. Det är här det är viktigt att man kan ha högerbarn / högergren utan att för den skull ha vänsterbarn / vänstergren!
Ofta lagras mer än enbart nyckeln i noden, t.ex. ett värde som ska associeras med nyckeln.
Ett lätt sätt att organisera datamängder för att lätt kunna söka upp information (om man redan känner till nyckeln).

Algoritm för sökning i ett binärt sökträd

Vi letar efter x i trädet t.

Om t är ett tomt träd finns inte x i det.
Om t är ett löv, finns x i trädet om och endast om x == nyckeln för t.
Om t inte är ett löv, och x < nyckeln för roten av t, fortsätt att söka i vänster gren.
Om t inte är ett löv, och x > nyckeln för roten av t, fortsätt att söka i höger gren.
Annars har vi en träff! (Vi vet att t inte är ett löv, och x är varken mindre eller större än nyckeln för roten av t.)

Hur kan vi använda dem i Python?

Det finns ingen implementation av binära sökträd i Pythons standardbibliotek. Om vi vill kunna arbeta med binära sökträd måste vi implementera dem själva, med andra ord skriva funktioner som gör allt det vi vill kunna göra med binära sökträd. För att kunna skriva dessa funktioner måste vi bestämma ett sätt att representera binära sökträd med hjälp av de inbyggda datatyperna i Python.

Representera binära sökträd med hjälp av listor

Vi antar att alla nycklar är heltal. Noder ska enbart lagra en nyckel (och hålla reda på eventuella barn), inte andra värden som associeras med nyckeln.
Det tomma trädet, utan noder, representeras av en tom lista.
Ett löv representeras direkt som en nyckel, dvs. ett heltal.
Inre noder representeras som [vänster gren, nyckel, höger gren]. Om en gren är tom sätts den till det tomma trädet.

Det finns många möjliga sätt att representera binära träd i Python, detta är endast ett av dem.

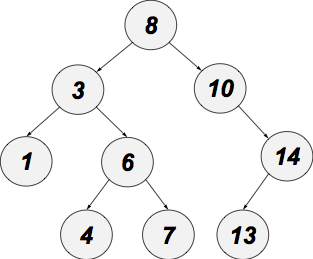
Här är vårt tidigare exempel representerat på detta vis.

[[1, 3, [4, 6, 7]], 8, [[], 10, [13, 14, []]]]

Primitiva funktioner

De primitiva funktionerna hjälper oss att implementera representationen. Var för sig är de ganska enkla, men de fungerar som gränssnitt gentemot andra funktioner som vill arbeta med binära sökträd.

def is_empty_tree(tree):
    return isinstance(tree, list) and not tree

def is_leaf(tree):
    return isinstance(tree, int)

def create_tree(left_subtree, key, right_subtree):
    return [left_subtree, key, right_subtree]

def left_subtree(tree):
    return tree[0]

def key(tree):
    if is_leaf(tree):
        return tree
    else:
        return tree[1]

def right_subtree(tree):
    return tree[2]

Rekursiv sökning i ett binärt sökträd

Vi implementerar nu den tidigare algoritmen i Python-kod. Notera att search() inte känner till representationen av trädet, utan endast de primitiva funktionerna. Denna abstraktion är viktig för att man t.ex. ska kunna ändra representationen av trädet utan att behöva ändra på search() och andra funktioner som använder binära sökträd.

def search(tree, x):
    """ Searches the tree for the key x """
    if is_empty_tree(tree):
        return False
    elif is_leaf(tree):
        return key(tree) == x
    elif key(tree) < x:
        return search(left_subtree(tree), x)
    elif key(tree) > x:
        return search(right_subtree(tree), x)
    else:
        return True

IDA - Institutionen för datavetenskap

Algoritmer

Introduktion

Sorteringsproblemet

Selection sort

Informell beskrivning

Illustration

Implementation

Insertion sort

Informell beskrivning

Illustration

Implementation

Rekursiva algoritmer

Induktiv metod

Anagramproblemets lösning

Tornet i Hanoi

Implementation

Lite om komplexitet

Quicksort

Informell beskrivning

Binära Träd

Binära sökträd (BST)

Algoritm för sökning i ett binärt sökträd

Hur kan vi använda dem i Python?

Representera binära sökträd med hjälp av listor

Primitiva funktioner

Rekursiv sökning i ett binärt sökträd