14. Problemlösning

Vi har hittills mest bara gått igenom hur de olika delarna av Python fungerar. På så sätt har vi lärt oss en massa om de byggstenar som ett program består av. Men hur ska man sätta ihop dem? Hur ska man egentligen tänka när man försöker skriva ett program? Det är en svår fråga, men vi ska nosa lite på den i det här kapitlet.

1. Programutvecklingsoprocessen

I den här kursen har vi än så länge skrivit rätt korta program som i princip bara består av en funktion. Då funkar det ganska bra att bara kasta sig över problemet och jobba hårt tills vi hittat en bra lösning. Men när du börjar skriva större program, och särskilt om du ska jobba tillsammans med andra, behöver arbetssättet vara betydligt mer strukturerat.

Det kanske är lite tidigt att börja tänka på detta, men vi ska redan nu zooma ut lite och titta på hur programutvecklingsprocessen kan se ut i sin helhet.

Ett sätt att beskriva hur man bör arbeta för att utveckla större program är vattenfallsmodellen. Den delar in arbetet i tydliga faser. Det finns många sätt att göra en sådan indelning och här är ett exempel:

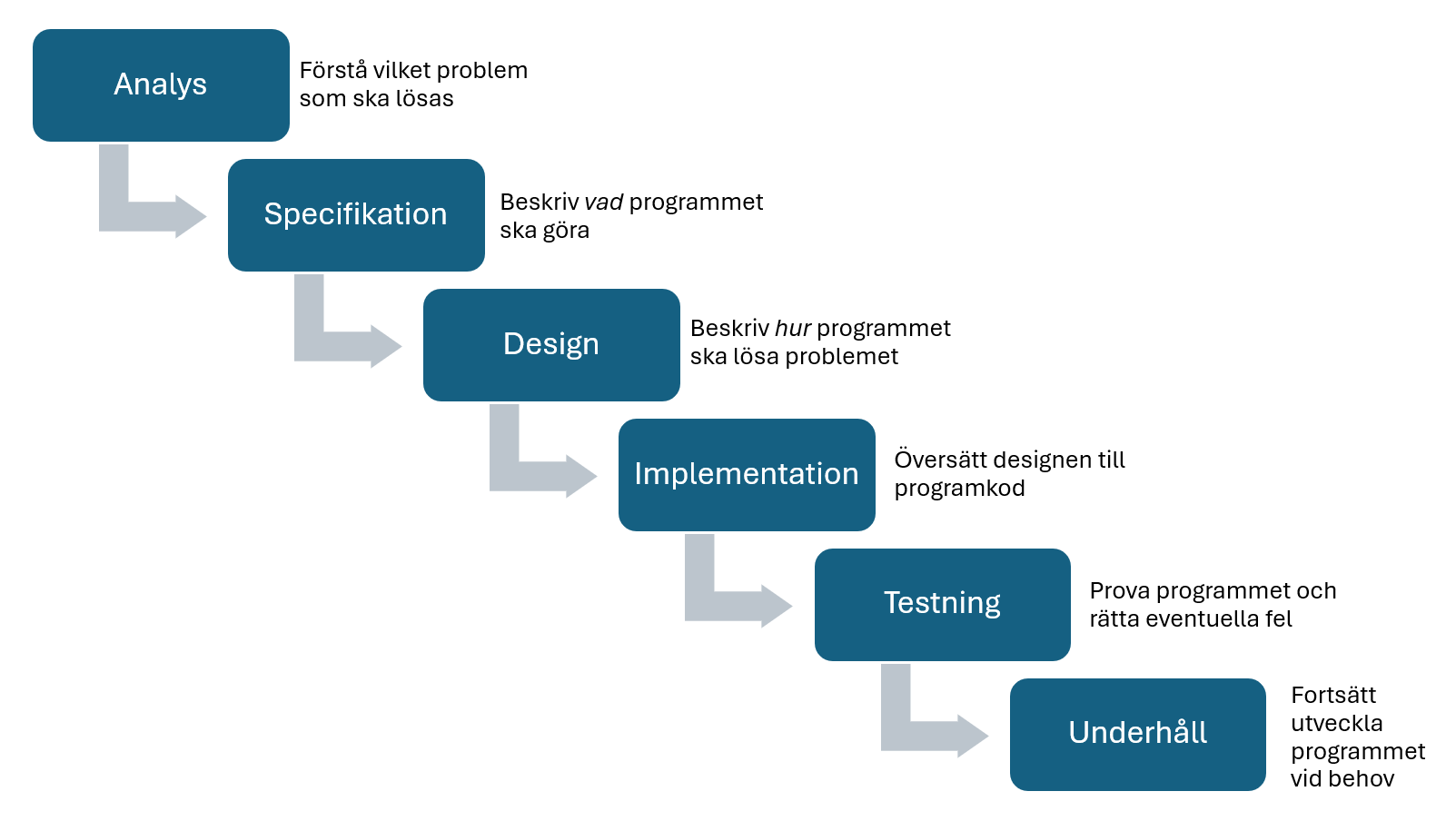
För att arbeta systematiskt ska vi alltså genomgå ett antal olika faser där resultatet av en fas liksom rinner ner till nästa fas. Det går inte att backa i den här processen, precis som ett vattenfall inte kan rinna uppåt.

Det här sättet att arbeta funkar bäst när man har riktigt stora ingenjörsprojekt, till exempel om man ska bygga en målraket. Det funkar dock inte riktigt lika bra för att utveckla programvara. Då används hellre så kallad agil utveckling.

Ordet agil betyder lättrörlig. En utvecklingsprocess som är agil är iterativ och inkrementell vilket betyder att man inte försöker bygga ett fullt fungerande system i ett svep, utan lite i taget. Arbetet delas upp i kortare sprintar som kan omfatta några dagar till några veckor. Varje sprint fungerar som ett varv i en cykel och innebär att man i miniformat går igenom de traditionella faserna från vattenfallsmodellen. På det här sättet finns det förhoppningsvis efter varje sprint en så kallad minimum viable product (MVP), en minsta livskraftig produkt, alltså en fungerande version som går att testa tidigt.

2. Exempel

De två modellerna från föregående avsnitt är förstås idealbilder. Verkligheten är inte alltid fullt så strikt. Och i den här introduktionskursen kommer vi inte att skriva så stora program att det är riktigt motiverat att dra igång en avancerad process. Men du kan ändå inspireras av de olika stegen. Grundtanken i båda modellerna är ju egentligen att vi ska tänka efter innan vi börjar koda, och det är alltid en bra idé.

Låt oss gå igenom ett kort exempel som illustrerar hur vi kan tänka utifrån de olika faserna.

Analys

Vi ska alltid börja med att försöka förstå vilket problem som ska lösas. Därför bör vi prata med den som har beställt programmet och ställa frågor för att få reda på vad man egentligen vill.

I vårt exempel heter beställaren Pelle. Han går just nu en kurs i EcoDriving för att bli bättre på att köra sin bil mer bränslesnålt. Han har tyvärr en gammal bil som inte visar hur mycket bensin den drar, men han vill ändå kunna hålla koll på bränsleförbrukningen. För att göra det hela lite mer spännande vill han ha ett Python-program som hjälper honom.

Specifikation

Nästa steg är att tänka genom problemet i lite mer detalj. Vad har vi till exempel för in- och utdata? Vilken funktionalitet behöver finnas? Detta säger än så länge inget om exakt hur vi åstadkommer det hela, bara vad vi vill ha.

Pelle säger att han vill ha ett enkelt program som tar en körd sträcka (i km) och hur mycket han har tankat (i liter). Programmet ska sedan räkna ut bränsleförbrukningen och skriva ut den.

Design

Nu är det till slut dags att tänka genom hur vi ska lösa problemet. Vi behöver fundera på hur funktionaliteten ska delas upp och hur olika delar av programmet ska prata med varandra. I små program som detta kan processen vara rätt så enkel och kanske till och med se uppenbar ut. I större program behöver man lägga ner större möda på att till exempel definiera hur information ska lagras internt.

Pelles program kommer att bestå av tre delar:

• Inmatning av information från användaren
• Uträkning av förbrukning enligt formeln förbrukning = bensinmängd/sträcka
• Utskrift av resultatet

Implementation

Nu är det äntligen dags att skriva kod! Återigen blir det ett väldigt enkelt exempel, nu med bara en enda funktion:

def fuel_efficiency():
    """ Lets the user input travel data and calculates the fuel efficiency """
    dist = eval(input("Distance (km): "))
    cons = eval(input("Consumption (l): "))
    eff = cons/(dist/10)
    print("Your car consumes ", eff, " liters per ten kilometers")

Testning

Innan vi levererar programmet till Pelle testar vi det, för att se att det fungerar i enlighet med de önskemål som Pelle formulerade i början av processen. Antalet tester beror på programmets komplexitet.

>>> fuel_efficiency()
Distance (km): 800
Consumption (l): 52
Your car consumes 0.65 liters per ten kilometers.

3. Pseudokod

De två tjusiga modellerna för programutveckling i stort hjälper oss inte särskilt mycket när det gäller det faktiska kodandet. Hur ska man tänka när man ska överföra en vag idé till programdkod? Ett sätt kan vara att skriva pseudokod.

Pseudokod är inte riktig kod och det finns egentligen ingen standard. Du kan hitta på vad som helst! Pseudokoden är ett mellanstadium mellan specifikationen (som uttrycker vad programmet ska göra i löpande text) och den färdiga programkoden. Den kan fungera som stödhjul för din tankeprocess. En del gillar att tänka i pseudokod, andra inte. Experiementera själv! Rita upp hur du tänker att programmet ska fungera innan du börjar! Penna och papper är bra hjälpmedel för detta.

Låt oss ta ett exempel. Tänk dig att vi ska implementera djupet först-sökning. Det är en algoritm för att söka efter information i en större datastruktur. Den ligger egentligen lite bortom vad du behöver kunna just nu, men den är lagom komplicerad för att vi ska kunna se skillnad mellan vanlig text, pseudokod och färdig programkod.

Om vi slår upp djupet först-sökning (DFS) kan vi få en textbeskrivning som ser ut så här:

Depth-first search (DFS) is an algorithm for traversing or searching tree or
graph data structures. The algorithm starts at the root node (selecting some
arbitrary node as the root node in the case of a graph) and explores as far
as possible along each branch before backtracking. 

Som vi ser är det här ganska vagt och uttrycker bara generella idéer. Vi kan försöka göra det tydligare genom att fortsätta beskriva algoritmen i ren text - eller så kan vi låna in begrepp från programmering och beskriva allt i pseudokod i stället. Då skulle det kunna se ut till exempel så här:

procedure DFS(G,v):
    label v as discovered
    for all directed edges from v to w that are in G.adjacentEdges(v) do
        if vertex w is not labeled as discovered then
            recursively call DFS(G,w)

Detta är helt klart ett mer precist uttryck för hur algoritmen ska fungera. Samtidigt har vi inte gått så långt som att beskriva exakt hur etiketter som discovered ska lagras, eller hur man tar alla bågar (eng. edges) och tar fram bara de som är riktade (eng. directed) och går från v till w. I stället har vi skrivit saker som:

• label ... as discovered
• for all directed edges from v to w that are in...
• if ... is not labeled as discovered ...

Det finns inget programspråk som förstår detta och kan utföra pseudokoden, men det är inte det som är tanken. Syftet är istället att:

• Innan implementationen är färdig: Hitta ett mellansteg där vi kan se om vår tänkta algoritm verkar stämma, utan att vi behöver gå ända ner till en fullständig implementation (som kanske har 10 eller 100 gånger så många rader kod). För att uppnå detta syfte måste vi skriva pseudokod på en nivå där vi förstår vad som ska göras. Det gjorde vi kanske inte från beskrivningen på ren engelska, men pseudokoden kan ge lagom mycket detaljer för att vi ska upptäcka eventuella tankemissar och felsteg innan vi lägger ner för mycket tid på att implementera.
• Efter att implementationen är färdig och testad: Ha ett sätt att beskriva algoritmen för andra, utan att binda sig till ett specifikt programmeringsspråk.

Det finns som sagt ingen definierad syntax för pseudokod, utan man skriver ner utformningen av det tilltänkta programmet på en form man själv är bekväm med. Experimentera och lär känna dig själv! Pseudokod kanske inte alls funkar för dig.

4. Söndra och härska

Ett annat bra tips för problemlösning är att tillämpa metoden söndra och härska eller divide and conquer som den heter på engelska. Grundtanken är att dela upp ett större problem i mindre delar. Dessa delar är oftast enklare problem att lösa än att försöka sig på att lösa hela problemet direkt. Lösningarna till de mindre delarna kan sedan kombineras till en lösning på det större problemet.

Tänk på följande:

1. Dela upp lösningen i flera funktioner så att varje funktion gör en sak och får ett vettigt namn. Använd samma terminologi i programkoden som används för att beskriva problemet. Det gör det enkelt att koppla ihop en funktion med en viss funktionalitet.
2. Gör varje funktion lagom stor. Det ska vara lätt att överblicka och testa varje funktion var för sig, men dela inte upp lösningen i för små delar. Gör man det kan det bli svårt att skapa sig en överblick, och koden kan bli onödigt ineffektiv.
3. Om det går, skriv funktioner som är generella och går att återanvända i andra projekt. Du tjänar oftast på att lösa lite större problem än du faktiskt har.

Exempel: Beräkning av perfekta tal

Vi säger att ett heltal k delar ett tal n om det finns ett heltal a sådant att a * k = n. Lite enklare kan man säga att k går jämnt upp i n. Vi säger att n är ett perfekt tal om summan av alla delarna är lika med n. Det finns inte särskilt många perfekta tal. De tre lägsta är:

• 6 (med delarna 1, 2 och 3)
• 28 (med delarna 1, 2, 4, 7 och 14)
• 496 (med delarna 1, 2, 4, 8, 16, 31, 62, 124 och 248)

Vi vill ha en Python-funktion perfect som tar reda på om ett heltal är perfekt eller inte. Hur kan vi dela upp problemet i mindre bitar?

Den här bilden illustrerar ett möjligt sätt att dela upp problemet.

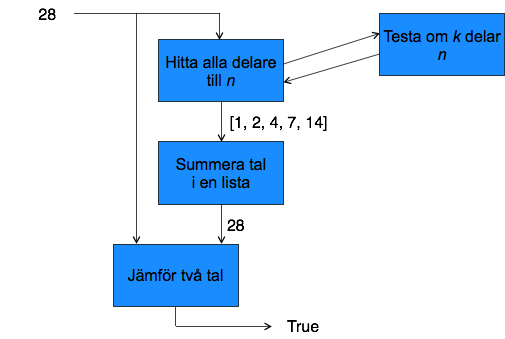
Vi ska implementera fyra olika funktioner:

• En funktion ska testa om ett tal k delar ett tal n. Det är antaligen inte så komplicerat, men det kan vara något som eventuellt kan återanvändas i annan kod, så vi lägger det i en separat funktion.
• En funktion ska hitta alla delarna till ett tal n. Den kommer att behöva använda den första funktionen.
• En funktion ska summera alla tal i en lista. Det låter som en uppgift som vi kan komma att behöva i andra program, så vi skriver en generell funktion. I just det här exemplet kommer listan att innehålla ett antal delare, men det spelar ju ingen roll för summeringen.
• En funktion ska utföra själva huvuduppgiften, alltså summera alla delarna för n och kolla om den summan är samma som n. I så fall är n ett perfekt tal.

Implementation

Nu när vi har identifierat hur vi kan dela upp problemet är det dags att implementera det. Vi börjar med det två första hjälpfunktionerna:

def divides(k, n):
    """ Checks if k divides n """
    return n % k == 0

def dividers(n):
    """ Return a list of all dividers of n """
    res = []
    for i in range(1, n//2+1)
        if divides(i, n):
            res = res + [i]
    return result

Vi testar dessa och ser att allt fungerar som förväntat:

>>> divides(3, 24)
True
>>> divides(2, 25)
False
>>> dividers(10)
[1, 2, 5]

Sedan fortsätter vi med resten av implementationen.

def sum_numbers(seq):
    """ Returns the sum of a list of numbers """
    if not seq:
        return 0
    else:
        return seq[0] + sum_numbers(seq[1:])

def perfect(n):
    """ Checks if n is a perfect number """
    return n == sum_numbers(dividers(n))

Och till sist testar vi helheten:

>>> sum_numbers([1, 2, 3, 4])
10
>>> sum_numbers(dividers(10))
8
>>> perfect(10)
False
>>> perfect(6)
True

Sammanfattning

• Om man zoomar ut lite och tänker på hur det går till att utveckla stora program så finns det två huvudsakliga modeller. Antingen kan man jobba enligt vattenfallsmodellen eller så kan man använda agil utveckling, vilket är det vanligaste i vår bransch.
• Som nybörjare i programmering har du kanske inte så stor nytta av att tänka på avancerade utvecklingsmodeller, men du kan ändå inspireras den grundläggande idén med de olika faserna. Det är alltid bra att tänka efter i förväg.
• Ett verktyg som kan hjälpa tanken är att skriva pseudokod. Det är ett informellt mellansteg mellan att beskriva problemet i ord och den färdiga programkoden.
• En strategi för att lösa större problem är att dela upp dem i mindre bitar enligt principen "söndra och härska".