6. Upprepning

En viktig grundmekanism i alla programspråk är upprepning. Vi behöver ofta upprepa saker, göra samma grej flera gånger, repetera någonting på ungefär samma sätt. I det här kapitlet ska vi titta lite närmare på två strategier för upprepning: iteration och rekursion.

1. En klassisk sångtext som exempel

99 Bottles of Beer är en småtråkig sång som man kan sjunga under långa utflykter. Den går ut på att man räknar ner från något tal, oftast runt 99. Och även om den klassiska varianten innebär att man räknar ölflaskor finns det givetvis alkoholfria alternativ också. Och texten säger faktiskt ingenting om att dricka ölen. Den går ungefär så här:

99 bottles of beer on the wall, 99 bottles of beer.
Take one down, pass it around. 98 bottles of beer.
98 bottles of beer on the wall, 98 bottles of beer.
Take one down, pass it around. 97 bottles of beer.
...

Du kan säkert föreställa dig resten.

Om vi vill skriva ett program som ska skriva ut texten så kan vi förstås skriva 198 print-satser i följd. Men ett smartare sätt vore att använda oss av särskilda programstrukturer för upprepning istället för att klippa och klistra. Lite längre fram ska vi se att det räcker med fyra rader kod. Dessutom blir koden mycket mer flexibel, eftersom vi kommer att kunna ange ett godtyckligt antal flaskor att börja med.

Vi vill skriva en funktion som räknar ner ett tal i från 99 till 1. För varje i ska den skriva ut de två sångraderna med i på rätt ställe. Vi vill ha något i denna stilen:

for i in range(???):
    print(???)

2. Hur fungerar range()?

Vi har tidigare använt for-satsen för att upprepa och funktionen range() för att ange hur många gånger något ska upprepas. Men hur fungerar range()? Det kan vi nog enklast visa med några exempel:

>>> for i in range(4):
...     print(i)
...
0
1
2
3
>>> list(range(4))
[0, 1, 2, 3]
>>> list(range(1,4))
[1, 2, 3]
>>> list(range(4,0,-1))
[4, 3, 2, 1]

Det finns tre olika sätt att använda range():

• range(slut) som ger en sekvens från 0 till men inte inklusive slut.
• range(start, slut) som ger en sekvens från start till men inte inklusive slut.
• range(start, slut, steg) som ger en en sekvens från start till men inte inklusive slut med steglängd steg.

start, slut och steg måste vara heltal. En tom sekvens ges om inget giltigt interall är givet.

Att vi använder list i exemplet ovan är bara ett trick för att enkelt få se hela intervallet. Python beräknar nämnligen inte hela intervallet, utan bara ett tal i taget.

3. Upprepning med iteration

När vi nu har lärt oss hur range() fungerar kan vi skriva en funktion som skriver ut vår låttext med hjälp av upprepning.

def song(n):
    for i in range(n,0,-1):
        print(f"{i} bottles of beer on the wall, {i} bottles of beer")
        print(f"Take one down, pass it around, {i-1} bottles of beer on the wall")

På rad 2 säger vi att i ska börja på n och gå ner till (men inte inklusive) 0. Vi använder -1 som steglängd, vilket ser till att vi räknar neråt istället för uppåt. På rad 3 och 4 skriver vi ut en del av låttexten med i insatt på rätt ställe. (Observera att det är viktigt att det står f innan strängen. Det innebär att det här är en särskilt formatterad sträng.) Dessa rader kommer att upprepas varje steg tills det att i har nått 0.

Som vi ser går det nu utmärkt att ange ett godtyckligt antal flaskor att börja med. Vi kan till exempel anropa song(1000) och börja med 1000 flaskor, utan att behöva klippa och klistra ett antal extra rader. Att skriva en generell funktion på det här sättet är värt att göra även om du från början bara hade 2-3 repetitioner. Det minskar också risken att du gör fel när du klipper och klistrar, och det visar intentionen bakom koden. Det syns direkt att vi ska göra nästan samma sak i varje steg (inga subtila skillnader i steg 42 som är lätta att missa), och det syns direkt vad som skiljer sig mellan de olika stegen (alltså i). Det blir lättare att se att koden faktiskt gör vad vi ville.

Det här sättet att åstadkomma upprepning kallas för iteration. Det är det enklaste och mest naturliga sättet. Det funkar för de allra flesta fall. Vi ska dock titta på ytterligare ett sätt att åstadkomma upprepning.

4. Upprepning med rekursion

En rekursiv funktion är en funktion som anropar sig själv.

Att åstadkomma upprepning med rekursion är lite krångligare och i de första exempel vi ska titta på här är iteration alltid bättre. Men det är bra att träna på rekursion, för lite längre fram kommer vi se exempel på upprening som bara kan lösas med rekursion.

Den stora poängen med rekursion är att lösa ett större problem genom att bryta ner svaret till mindre instanser av samma problem. För att börja nosa lite på begreppet gör vi först bara en enkel variant. Här beräknar vi egentligen aldrig lösningen på något delproblem. I stället gör vi utskrifter. Så här kan då en rekursiv variant av sången se ut:

def song(i):
    if i > 0:
        print(f"{i} bottles of beer on the wall, {i} bottles of beer")
        print(f"Take one down, pass it around, {i-1} bottles of beer on the wall")
        song(i - 1)

På rad 3-4 gör vi samma sak som i den iterativa varianten, vi skriver ut låttexten och skriver in i på rätt ställe. Efter att vi har skrivit ut texten för ett visst i så anropar vi funktionen igen med i-1. Har vi nyss skrivit ut texten där i är 8 så vill vi nu skriva ut den för fallet där i är 7.

För att se till att funktionen någon gång slutar anropa sig själv har vi på rad 1 en if-sats som ser till att koden bara körs om song() anropas med ett i som är större än 0. Försäkra dig själv om att funktionen körs för evigt om if-satsen inte är där!

Iteration och rekursion när man beräknar ett värde

Men varför vill man upprepa med hjälp av rekursion?

Ofta vill man inte det. Men tänk dig att vi inte vill skriva ut något utan i stället vill beräkna ett värde. Vi vill skapa en lista som innehåller alla textrader i sången.

I en iterativ version kan det se ut så här:

def song(n):
    result = []
    for i in range(n,0,-1):
        result.append(f"{i} bottles of beer on the wall, {i} bottles of beer")
        result.append(f"Take one down, pass it around, {i-1} bottles of beer on the wall")
    return result

Variabeln result är en lista av strängar. Varje gång vi gör result.append() så läggs en ny sträng till sist i listan.

I en rekursiv version kan vi istället göra så här:

def song(i):
    if i == 0:
        return []
    else:
        return [f"{i} bottles of beer on the wall, {i} bottles of beer",
                f"Take one down, pass it around, {i-1} bottles of beer on the wall"] + song(i - 1)

Här har vi först ett basfall där vi har 0 flaskor kvar. Då är sångtextlistan tom och vi returnerar tomma listan [].

Vi har sedan ett fall där vi har minst en flaska kvar. Hur ska vi lösa detta? Jo, vi vet vilka textrader som ska vara först om man börjar med exakt i flaskor -- de två strängarna som vi lägger i en första lista i koden ovan. Sedan kan vi ju göra ett anrop till song(i-1) för att få reda på hur man fortsätter när man har druckit upp en flaska och bara har i-1 flaskor kvar.

Vi har alltså löst en del av problemet och skjuter resten av det framför oss med ett rekursivt anrop.

5. Fakultet

För att ytterligare illustrera skillnanderna mellan iterativ och rekursiv upprepning ska vi ta ett exempel till, den matematiska fakultetsfunktionen. Återigen, för de här exemplen är iteration nästan alltid bättre, men längre fram kommer vi att se exempel där rekursion är det enda möjliga valet. Då är det bra att ha övat rekursion på enklare funktioner.

Iterativ version

Fakulteten av n är produkten av alla tal från 1 till n, där n>=1.

n! = n x (n - 1) x (n - 2) x ... x 2 x 1

Hur kan man skriva detta i Python-kod?

def factorial(n):
    res = 1
    for i in range(2, n + 1):
        res = res * i
    return res

Vi börjar med att sätta resultatet till 1. På rad 3 säger vi sedan att vi vill gå igenom alla tal från 1 till (men inte inklusive) n+1. Inuti for-loopen multiplicerar vi varje sådant tal på resultatet (rad 4). Till slut skickar vi tillbaka resultatet med en return-sats. Vi testar programmet:

>>> factorial(5)
120

Rekursiv version

Vi upprepar definitionen av rekursion (men hoppar över specialfallet n=0 just nu):

n! = n x (n - 1) x (n - 2) x ... x 2 x 1

Detta gäller för alla n. Om vi antar att k är minst 2, och sätter in n=k och n=k-1, kan vi se att:

k! = k x (k - 1) x (k - 2) x ... x 2 x 1

(k-1)! = (k - 1) x (k - 2) x ... x 2 x 1

Som du ser är (k-1)! lika med den högra delen av definitionen av k!. Med andra ord har vi att:

k! = k * (k - 1)!

givet att k>=2. Och om k=1 vet vi redan att k!=1.

Alltså kan vi skriva att k! är:

• 1 om k är 1,
• k * (k-1)! annars.

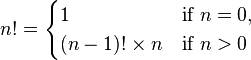
Här är det återigen så att man kan lösa ett problem om man vet svaret till mindre instanser av samma problem. Om vi vet (k-1)! kan vi snabbt räkna ut k! genom en extra multiplikation.

Hur kan man skriva det i Python-kod?

def factorial(k):
    if k == 1:
        return 1
    else:
        return k * factorial(k - 1)

Den första raden i raden i den matematiska definitionen är basfallet som ser till att rekursionen slutar. Här ser vi att rad 2-3 i Python-koden är basfallet. Vi kollar här ifall k är lika med 1, är detta sant så returnerar vi 1. Alla rekursiva funktioner måste ha ett basfall för att se till rekursionen slutar.

Rekursionsfallet (den nedre raden i den matematiska definitionen) motsvaras av rad 4-5 i Python-koden. Här returneras värdet av k multiplicerat med fakulteten av k-1. För att räkna ut fakulteten av k-1 så använder vi factorial-funktionen igen. Rekursionsfallet måste se till att problemet går mot basfallet.

Missa inte att rekursionen löste ett delproblem av samma typ! För att räkna ut ett fakultetsproblem fick man också räkna ut ett annat fakultetsproblem. Det är detta som identifierar en rekursiv lösningsmodell.

Sammanfattning

• Upprepning kan lösas iterativt med for-satsen.
• För att tala om hur många gånger något ska upprepas kan vi använda funktionen range().
• Upprepning kan också lösas rekursivt med en funktion som anropar sig själv.
• Vid rekursion behövs ett basfall så att rekursion stannar någon gång.

Extramaterial

Quiz om upprepning