Göm menyn

3. Dictionaries och rekursion

3.1 Redovisning

Från och med laboration 3 och framåt går redovisningen till så här:

  1. Muntlig redovisning för labbassistenten under schemalagda labbtider
  2. Incheckning av din kod i git-repot (se mer info nedan)
  3. Meddela labbassistenten att du checkat in genom att skapa ett ärende i git (Klicka här!)

Hur vi använder git

Från och med laboration 3 ska du använda ett git-repo (ett filarkiv för versionshantering) som vi har skapat åt dig för att du enkelt ska kunna skicka in din kod. Just nu behöver du inte förstå alla detaljer kring detta repo. Det återkommer vi till senare i kursen. Det räcker med att du följer med i de kommandon vi visar dig.

För att komma igång behöver du först klona repot. Det gör du genom följande steg:

  1. Förflytta dig till katalogen där du vill ha repot.

    2. Exempel: cd ~/kurser/tdde23

  2. Kör följande kommando:

    3. git clone [url_till_repo]

    Exempel: git clone https://gitlab.liu.se/tdde23-2021/tdde23-2021-labbar-xx-xx-x-xx.git

URL till ditt eget git-repo får du via e-post när repot har skapats. Det skapas av oss, genom ett script, en tid efter att du har gjort din första inloggning på gitlab.liu.se.

När du har kört git clone är det bara att jobba på som vanligt i filerna i den nya katalogen som har skapats. Om något känns oklart kan du ta hjälp av din labbassistent.

Alla laborationer från nu och framåt ska, förutom att redovisas muntligt, även skickas in till assistenten, så att du kan få mer detaljerad återkoppling på din kod.

För att göra det utför du följande sekvens av kommandon, när du står i katalogen för repot:

  1. git add -A
  2. git commit -m "meddelande"

    3. Exempel: git commit -m "finish lab 3"

  3. git push

Dessa tre steg kommer att kopiera din kod, dina filer, till git så att din labassistent enkelt kan hämta hem allt därifrån och testköra i lugn och ro.

Utöver att checka in koden enligt beskrivningen ovan ska du också meddela labassistenten att du är klar genom att skapa ett ärende. Läs mer om detta på sidan för Regler för redovisning och komplettering.

3.2 Inledning

Studiematerial

Innan denna labb påbörjas bör följande studiematerial ha lästs:

I den andra laborationen övade du på iteration över tal och raka listor. I den här laborationen tränas iterativa och rekursiva sätt att bearbeta mer andra datastrukturer, som tupler (immuterbara listor) och dictionaries

Den här labbomgången innehåller fler övningar än du troligtvis kommer hinna med att göra. Du får själv prioritera vilka som är viktigast för dig, så att du hinner med uppgifterna som ska redovisas.

3.3 Förberedande övningar

I detta avsnitt introduceras typerna tupel och dictionary, och ett par små men viktiga detaljer om tillåtna värden repeteras.

Övning 301 Tupler fungerar i princip på samma sätt som listor, men med två noterbara undantag. Den första skillnaden är att tupler står inom vanliga parenteser istället för hakparenteser. Den andra skillnaden kommer du att upptäcka i den här övningen. Tupler kan, precis som listor, innehålla vilka typer av data som helst. Här har vi ett par exempel på representationer av (x, y)-koordinater.

>>> pos_one = (5, 0) >>> pos_two = ('fem', 'noll') >>> pos_three = ([5], [0])

Skriv kommandon som tar fram x-koordinaten respektive y-koordinaten ur var och en av de tre tuplerna ovan. Hur ändrar man koordinaten för pos_one till (5, 5), om det överhuvudtaget är möjligt? Kan det ändras "på plats", utan att använda uttryck som pos_one = ... på liknande sätt som man ändrar enstaka element i en lista? Kan du göra motsvarande med de andra tuplerna?

Övning 302 I en dictionary parar man ihop en nyckel med data. Därefter kan man ta fram data genom att använda nyckeln. Man kan tänka på dem som en slags avancerade listor där man, istället för att använda ett tal som index, använder i princip vilken typ av data som helst. Prova att skriva in följande:

>>> numbers = {"one": 1, "two": 2, "seven": 6, "eight": 9} >>> numbers["one"] 1

För att bekanta dig med hur man använder dictionaries, skriv nu kommandon som gör följande:

  • lägger till nyckeln "three" kopplat till lämplig siffra i numbers.
  • ändrar så att numbers["eight"] ger siffran 8

Övning 303 Här nedanför ser du två sätt att försöka skapa dictionaries. Ett av dem fungerar, det andra gör det inte. Försök förutse vilket som fungerar. Pröva sedan att skriva in det vid Python-prompten och se om du hade rätt.

>>> coodinates_one = { (1, 0, 0): "x-axis", (0, 1, 0): "y-axis" } >>> coordinates_two = { [1, 0, 0]: "x-axis", [0, 1, 0]: "y-axis" }

Varför fungerar bara det ena? Försök också hitta en lista eller tupel (det av exemplen som fungerade här ovanför) som inte fungerar att ha som nyckel.

Övning 304 I den första övningen använde vi tupler för att lagra koordinater. Detta fungerar bra, men för att plocka ut x-koordinaten respektive y-koordinaten ur en sådan tupel behöver man indexera med ett inte särskilt informativt heltal -- man behöver komma ihåg vad som finns på index 0 och index 1. Om man har fler värden i en tupel kan det vara svårare att komma ihåg vad som finns var.

Ett alternativ är att använda dictionaries istället för tupler. Då kan de olika värdena namnges istället för att indexeras. Här har vi ett par exempel på representationer av (x, y)-koordinater i form av dictionaries.

>>> pos_one = { "x": 5, "y": 0 } >>> pos_two = { "x": 'fem', "y": 'noll' } >>> pos_three = { "x": [5], "y": [0] }

Skriv kommandon som tar fram x-koordinaten respektive y-koordinaten ur var och en av de tre dictionaries ovan. Hur ändrar man koordinaten för pos_one till (5, 5), om det överhuvudtaget är möjligt? Kan det ändras "på plats", utan att använda uttryck som pos_one = ... på liknande sätt som man ändrar enstaka element i en lista?

Att använda dictionaries på detta sätt kan i vissa fall vara "overkill", men ofta är det till stor hjälp att olika värden får *namn* istället för bara *index* -- inte minst när man ska läsa koden, felsöka den, eller gå in och ändra i tidigare skriven kod. Är person[7] eller person["birthdate"] lättare att förstå? Är de extra tecknen man behöver skriva värt detta?

3.4 Spelbräde

Uppgift 3A - Spelbräde

Målet med uppgiften är att du ska kunna använda dictionaries och tupler för att skapa ett antal funktioner som tillsammans hanterar en datatyp.

Bakgrund

Låt oss tänka att vi ska skriva ett spel där vi ska placera ut relativt få spelfigurer på ett väldigt stort bräde, säg en karta som omfattar 100 000 x 100 000 rutor.

En första tanke vore att göra som i det mindre problemet; att representera det hela som en matris med listor i listor. En tom plats blir en nolla i matrisen och en figur markeras med ett spelarnamn, till exempel. Det kan ha sina fördelar, men fungerar inte så bra när skalan ökar. Säg att vi har fem spelare med 200 figurer var på kartan ovan. Det blir totalt 1000 symboler och inte mindre än 99 999 000 tomma rutor att lagra.

För att slippa lagra en massa tomma rutor explicit kan ett alternativ vara att knyta ihop varje figur och dess position på något sätt. På det sättet får vi 1000 saker att lagra istället för 100 000 000. Alla rutor som inte explicit har någon markering antas då vara tomma, och vi har sparat massor av minnesutrymme.

Själva uppgiften

Din uppgift är att med hjälp av denna insikt, och den nyligen introducerade dictionary-typen, hitta på ett sätt att representera spelbrädet på ett smart sätt. I praktiken innebär det att du ska konstruera följande funktioner: new_board (skapar ett nytt spelbräde), is_free (kollar om en viss plats är ledig), place_piece (placerar en figur på en plats), get_piece (returnerar pjäsen på en viss plats), remove_piece, move_piece, count, nearest_piece (returnera den närmsta pjäsen, och finns det fler pjäser på samma avstånd är det fritt att välja vilken som).

Ditt program ska fungera enligt det belysande exemplet nedan. Här har vi som exempel valt att pjäserna är antingen strängen "spelare1" eller "spelare2", men det kan förstås vara vilja strängar som helst.

Var noga med vilket av argumenten som representerar rad (y-koordinat) och vilket som representerar kolumn (x-koordinat)!

>>> board = new_board() >>> is_free(board, 500, 100) # Är platsen på kolumn 500 och rad 100 ledig? True >>> place_piece(board, 500, 100, "spelare1") # Placera en figur från "spelare1" på position (500, 100). True >>> place_piece(board, 1, 100, "spelare2") True >>> place_piece(board, 500, 100, "spelare2") # Försök placera en figur på en redan upptagen position. False >>> place_piece(board, 500, 200, "spelare2") True >>> is_free(board, 500, 100) False >>> get_piece(board, 500, 100) 'spelare1' >>> get_piece(board, 666,666) False >>> remove_piece(board, 500, 100) # Ta bort figuren på plats (500, 100). True >>> remove_piece(board, 1, 1) # Det fanns ingen figur på den platsen. False >>> is_free(board, 500, 100) True >>> move_piece(board, 500, 200, 500, 100) # Flytta pjäsen på (500, 200) till (500, 100). True >>> get_piece(board, 500, 100) 'spelare2' >>> count(board, "column", 500, "spelare2") # Räkna antalet figurer av typen "spelare2" i kolumn 500. 1 >>> count(board, "row", 100, "spelare2") # Räkna antalet figurer av typen "spelare2" på rad 100. 2 >>> nearest_piece(board, 500, 105) # Hitta figuren närmast position (500, 105). (500, 100)

Några tips

Känns det här stort och svåröverskådligt? Ta det lugnt. Här kommer några tips på vägen.

  • För att räkna ut avståndet mellan två koordinater i den sista funktionen ovan, använd Pythagoras sats.
  • Läs igenom körexemplet ovan ordentligt. Det visar allt som du behöver kunna göra med spelbrädet. Testa dina idéer på hur spelbrädet ska representeras mot dessa. Funktionerna ska returnera precis det som står i exemplet. Försöker du använda samma nyckel flera gånger? Går det att se till att man behöver leta genom färre figurer? Det finns många sätt att resonera här!
  • När vi väl har definierat en funktion som utför en viss sak, ska den funktionen alltid användas för att utföra denna sak. Till exempel är det alltid is_free som ska användas om man vill veta om en viss position är ledig, inte bara i kod som använder våra funktioner utan även inom de övriga funktionerna som du skriver i denna uppgift. Detta har (minst) tre fördelar. För det första slipper man upprepa kod som implementerar en viss funktionalitet. För det andra bygger man upp sin kod med meningsfulla begrepp som is_free istället för att gå direkt på en intern representation på låg nivå. För det tredje blir det oftast enklare att ändra koden om allt som har med "lediga platser" att göra ligger i en enda funktion, istället för att vara utspritt över många funktioner.

OBS! Denna kurs behandlar inte objektorientering. Om det är något du sysslat med tidigare, lägg inte tid på att kapsla in bräden och dylikt i klasser. Det ingår inte i uppgiften!

Testning För att se till att din funktion klarar av uppgiften finns det ett Pythonprogram som kör automatisk testning på din kod. Programmet ligger i filen test3.py och finns redan i ditt Git-repo. Öppna filen och läs instruktionerna för hur man för att se hur man kör programmet och kör det sedan för att testa labb 3A.

Du får gärna fråga handledaren om något är oklart. I övrigt väntar vi med demonstration och inlämning till du är klar med hela labb 3.

3.5 Upprepning med rekursion

I förra laborationsomgången använde vi oss av iteration för att utföra upprepningar. Nu ska vi lösa samma övningar, fast genom att utnyttja rekursion.

Övning 304 Definiera rekursiva funktionen "upphöjt till". Kalla den power och låt den ta två heltalsargument. Funktionen ska vara rekursiv, d.v.s. du får inte använda konstruktioner som for eller liknande.

>>> power(2, 3) 8 >>> power(5, 2) 25

Du kan testa att du gjort rätt genom att jämföra med den inbyggda operatorn ** som beräknar just "upphöjt till". (Givetvis får du inte använda dig av den i funktionen power.)

Övning 305 Definiera en rekursiv funktion sum_first som adderar ihop de första n heltalen. Summan av de n första heltalen kan också beräknas med formeln n(n+1)/2 men i den här övningen vill vi att du summerar talen ett i taget med hjälp av någon form av upprepning (rekursion). Funktionen ska även här vara rekursiv, d.v.s. du får inte använda konstruktioner som for eller liknande.

>>> sum_first(6) 21 >>> sum_first(0) 0

Övning 306 Skriv en funktion sum_numbers som summerar de element på en lista som är tal. Allt annat som finns på listan ska ignoreras. Denna övning ska lösas rekursivt.

Så här kontrollerar du om något är ett tal:

import numbers def is_number(x): return isinstance(x, numbers.Number)

Nu kan du testa om saker är tal med anrop som is_number(5.324).

>>> sum_numbers(["a", 1, "b", 2, [["b", 4], 2], 3]) 6

Övning 307 Skriv en funktion find_letter som returnerar ett sant värde (True) om en given bokstav (egentligen en sträng) finns i ett ord, annars ett falskt värde (False). Ordet representeras som en lista. Denna övning ska lösas rekursivt.

>>> find_letter("u", ["h", "u", "s"]) True >>> find_letter("a", ["b", "i", "l"]) False

Övning 308 Skriv en funktion remove_vowels som tar en lista med bokstäver (egentligen strängar) och returnerar en ny lista med vokalerna borttagna. Det kanske går lättare om du föreställer dig att du ska skapa en ny lista med endast konsonanter snarare än att ta bort vokalerna. Denna övning ska lösas rekursivt. Tips: Använd dig av find_letter som du definierat ovan!

>>> remove_vowels(["b", "i", "r", "g", "i", "t", "t", "a"]) ['b', 'r', 'g', 't', 't']

Övning 309 Skriv en rekursiv funktion range_product som beräknar produkten av alla heltal från nmin till nmax. Produkten av heltal från 2 till 5 räknas inklusive gränserna, och är alltså 2 * 3 * 4 * 5 = 120. Denna övning ska lösas rekursivt.

>>> range_product(5, 10) 151200

Övning 310 Skriv en funktion factorial som beräknar fakulteten av ett heltal n. Fakulteten av 0 definieras som 1. Funktionen ska vara rekursiv, och får gärna anropa funktioner du definierat tidigare.

>>> factorial(5) 120 >>> factorial(0) 1

Uppgift 3B - Pokerhänder

Målet med uppgiften är att du ska kunna lösa matematiska problem med programmering genom att iterera över tal.

En pokerhand består av 5 kort och en kortlek har 52 kort. Hur många olika pokerhänder kan dras ur en vanlig kortlek? Mer allmänt, på hur många sätt kan man välja k element bland n stycken, utan återläggning och utan att ordningen bland de k elementen spelar roll? Som man får lära sig i grundkurser i diskret matematik är svaret (n k) vilket utläses "n över k" och definieras så här:

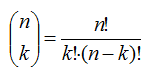
Din uppgift är att skriva en rekursiv funktion choose som tar två positiva heltal n och k (n >= k) och ger (n k). Lösningen ska vara strikt funktionell, och du får inte använda konstruktioner som for eller liknande.

En klurighet är att din funktion ska klara relativt stora tal. Om man inte tänker efter kan detta göra att delberäkningar blir väldigt - till och med ohanterligt - stora, även om det slutliga svaret är hanterbart.

>>> choose(5, 3) 10 >>> choose(1000, 1) 1000 >>> choose(52, 5) 2598960 >>> choose(1000, 4) 41417124750 >>> choose(1000, 800) 661715556065930365627163346132458831897321703017638669364788134708891795956 726411057801285583913163781806953211915554723373931451847059830252175887712 457307547649354135460619296383882957897161889636280577155889117185 >>> choose(1000, 999) 1000

Börja gärna med att skriva ned - på papper - hur du beräknar (10 3), (10 5), (10 7), (10 1). Finns det några förenklingar eller omskrivningar som du kan göra? Finns det några tal som blir likadana, men där den ena beräkningen är mycket lättare att göra?

Testning För att se till att din funktion klarar av uppgiften finns det ett Pythonprogram som kör automatisk testning på din kod. Programmet ligger i filen test3.py och finns redan i ditt git-repo. Öppna filen och läs instruktionerna för hur man för att se hur man kör programmet och kör det sedan för att testa labb 3B.

Demonstrera både labb 3A och labb 3B för handledaren. Skicka därefter in den demonstrerade programkoden för samtliga funktioner du skrivit i uppgifterna 3A och 3B, samt representativa körexempel. Inlämningen sker genom att skicka upp filerna till git (instruktioner om hur man gör detta finner du längst upp på den här sidan) och sedan skapa ett inlämningsärende. I detta ärende fyller du i URL till ditt repo (samma som angavs vid "git clone") och vilka labbar som du vill lämna in.


Sidansvarig: Peter Dalenius
Senast uppdaterad: 2023-09-20