Hide menu

Partial Differential Equations (PDEs) in Modelica

In Modelica, models are defined using equations and connections between components. Equations containing time-dependent variables, i.e. single variable functions, and time derivatives of such functions are supported, so that a system of ordinary differential and algebraic equations (DAE) is specified. However, in many engineering applications, there are models and simulation of systems that involve multi-variable functions containing partial derivatives and partial differential equations (PDEs). Extending Modelica to support modeling of such systems makes it usable for a larger set of modeling and simulation applications.
The goal of this project is to investigate, design and evaluate the extensions to the Modelica language that are needed to support modeling with PDE and specification of problems containing PDE, such as initial and boundary value problems.  Also, the connection mechanism in Modelica will be generalized to support multi-dimensional connections. Furthermore, connections between DAE-based models that already are supported in Modelica, and PDE-based models will be defined, in order to support integrating PDE models with already existing Modelica models.
 

PDEs that can be specified should have generic form, for instance, 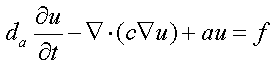where some components can be zeroes.

In order to specify models containing partial differential equations, the concept of domains and domain boundaries are needed in the language. A domain can be defined by describing its boundary. A new kind of Modelica class can be used to represent domains, with a section called boundary that describes its boundary using lines and parametric curves. A construct for composing separately defined boundaries is also needed, in order to describe more complex domains and also to assign boundary conditions to specific boundary parts. For example, an arc that can be used when defining domains can be written as follows: 

domain Arc
 parameter Real r=1, a=1;
boundary
 curve(r*cos(a*u),
       r*sin(a*u)) where u in (0,2*PI);
end Arc;
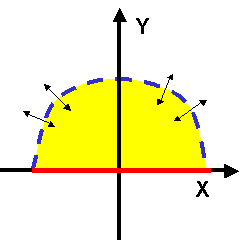
A domain consisting of an arc an a line can then be defined as: 
domain HalfCircle
 Arc arc(a=0.5, r=2);
 Line line(x0=-2, y0=0, x1=2, y1=0);
boundary
 composite(arc, line);
end Arc;
Boundary conditions can be assigned to this domain using the names of the components, as follows: 
model PDEModel
    HalfCircle mydomain;
    ...
equation
    mydomain.line.bc = isolated;
    mydomain.arc.bc = conducting;
end HalfCircle;
Software we use for solution:
  • bamg, bidimensional mesh generator
  • rheolef, Finite element environment (C++, Unix)
Typical PDE solution

Page responsible: Webmaster
Last updated: 2012-05-07