This package contains basic analog electrical components:
Modelica.Electrical.Analog.Basic.Ground
Ground of an electrical circuit. The potential at the ground node is zero. Every electrical circuit has to contain at least one ground object.
model Ground "Ground node" Interfaces.Pin p; equation p.v = 0; end Ground;
Modelica.Electrical.Analog.Basic.Resistor
The linear resistor connects the branch voltage v with the branch current i by i*R = v. The Resistance R is allowed to be positive, zero, or negative.
| Name | Default | Description |
|---|---|---|
| R | 1 | Resistance [Ohm] |
model Resistor "Ideal linear electrical resistor" extends Interfaces.OnePort; parameter SI.Resistance R=1 "Resistance"; equation R*i = v; end Resistor;
Modelica.Electrical.Analog.Basic.HeatingResistor
This is a model for an electrical resistor where the generated heat is dissipated to the environment via connector heatPort and where the resistance R is temperature dependent according to the following equation:
R = R_ref*(1 + alpha*(heatPort.T - T_ref))
alpha is the temperature coefficient of resistance, which is often abbreviated as TCR. In resistor catalogues, it is usually defined as X [ppm/K] (parts per million, similarly to per centage) meaning X*1.e-6 [1/K]. Resistors are available for 1 .. 7000 ppm/K, i.e., alpha = 1e-6 .. 7e-3 1/K;
When connector heatPort is not connected, the temperature dependent behaviour is switched off by setting heatPort.T = T_ref. Additionally, the equation heatPort.Q_dot = 0 is implicitly present due to a special rule in Modelica that flow variables of not connected connectors are set to zero.
| Name | Default | Description |
|---|---|---|
| R_ref | Resistance at temperature T_ref [Ohm] | |
| T_ref | 300 | Reference temperature [K] |
| alpha | 0 | Temperature coefficient of resistance [1/K] |
model HeatingResistor "Temperature dependent electrical resistor"
extends Interfaces.OnePort;
parameter SI.Resistance R_ref "Resistance at temperature T_ref";
parameter SI.Temperature T_ref=300 "Reference temperature";
parameter Real alpha(unit="1/K") = 0 "Temperature coefficient of resistance";
SI.Resistance R "Resistance = R_ref*(1 + alpha*(heatPort.T - T_ref));";
Modelica.Thermal.HeatTransfer.Interfaces.HeatPort_a heatPort;
equation
v = R*i;
if cardinality(heatPort) > 0 then
R = R_ref*(1 + alpha*(heatPort.T - T_ref));
heatPort.Q_dot = -v*i;
else
/* heatPort is not connected resulting in the
implicit equation 'heatPort.Q_dot = 0'
*/
R = R_ref;
heatPort.T = T_ref;
end if;
end HeatingResistor;
Modelica.Electrical.Analog.Basic.Conductor
The linear conductor connects the branch voltage v with the branch current i by i = v*G. The Conductance G is allowed to be positive, zero, or negative.
| Name | Default | Description |
|---|---|---|
| G | 1 | Conductance [S] |
model Conductor "Ideal linear electrical conductor" extends Interfaces.OnePort; parameter SI.Conductance G=1 "Conductance"; equation i = G*v; end Conductor;
Modelica.Electrical.Analog.Basic.Capacitor
The linear capacitor connects the branch voltage v with the branch current i by i = C * dv/dt. The Capacitance C is allowed to be positive, zero, or negative.
| Name | Default | Description |
|---|---|---|
| C | 1 | Capacitance [F] |
model Capacitor "Ideal linear electrical capacitor" extends Interfaces.OnePort; parameter SI.Capacitance C=1 "Capacitance"; equation i = C*der(v); end Capacitor;
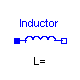
Modelica.Electrical.Analog.Basic.Inductor
The linear inductor connects the branch voltage v with the branch current i by v = L * di/dt. The Inductance L is allowed to be positive, zero, or negative.
| Name | Default | Description |
|---|---|---|
| L | 1 | Inductance [H] |
model Inductor "Ideal linear electrical inductor" extends Interfaces.OnePort; parameter SI.Inductance L=1 "Inductance"; equation L*der(i) = v; end Inductor;
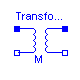
Modelica.Electrical.Analog.Basic.Transformer
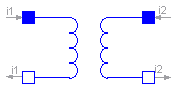
The transformer is a two port. The left port voltage v1, left port current i1, right port voltage v2 and right port current i2 are connected by the following relation:
| v1 | | L1 M | | i1' |
| | = | | | |
| v2 | | M L2 | | i2' |
L1, L2, and M are the primary, secondary, and coupling inductances respectively.
| Name | Default | Description |
|---|---|---|
| L1 | 1 | Primary inductance [H] |
| L2 | 1 | Secondary inductance [H] |
| M | 1 | Coupling inductance [H] |
model Transformer "Transformer with two ports" extends Interfaces.TwoPort; parameter SI.Inductance L1=1 "Primary inductance"; parameter SI.Inductance L2=1 "Secondary inductance"; parameter SI.Inductance M=1 "Coupling inductance"; equation v1 = L1*der(i1) + M*der(i2); v2 = M*der(i1) + L2*der(i2); end Transformer;
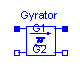
Modelica.Electrical.Analog.Basic.Gyrator
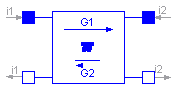
A gyrator is a two-port element defined by the following equations:
i1 = G2 * v2
i2 = -G1 * v1
where the constants G1, G2 are called the gyration conductance.
| Name | Default | Description |
|---|---|---|
| G1 | 1 | Gyration conductance [S] |
| G2 | 1 | Gyration conductance [S] |
model Gyrator "Gyrator" extends Interfaces.TwoPort; parameter SI.Conductance G1=1 "Gyration conductance"; parameter SI.Conductance G2=1 "Gyration conductance"; equation i1 = G2*v2; i2 = -G1*v1; end Gyrator;
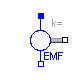
Modelica.Electrical.Analog.Basic.EMF
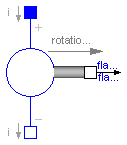
EMF transforms electrical energy into rotational mechanical energy. It is used as basic building block of an electrical motor. The mechanical connector flange_b can be connected to elements of the Modelica.Mechanics.Rotational library. flange_b.tau is the cut-torque, flange_b.phi is the angle at the rotational connection.
| Name | Default | Description |
|---|---|---|
| k | 1 | Transformation coefficient [N.m/A] |
model EMF "Electromotoric force (electric/mechanic transformer)" parameter Real k(final unit="N.m/A") = 1 "Transformation coefficient"; SI.Voltage v "Voltage drop between the two pins"; SI.Current i "Current flowing from positive to negative pin"; SI.AngularVelocity w "Angular velocity of flange_b"; Interfaces.PositivePin p; Interfaces.NegativePin n; Modelica.Mechanics.Rotational.Interfaces.Flange_b flange_b; equation v = p.v - n.v; 0 = p.i + n.i; i = p.i; w = der(flange_b.phi); k*w = v; flange_b.tau = -k*i; end EMF;
Modelica.Electrical.Analog.Basic.VCV
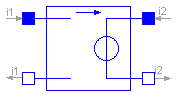
The linear voltage-controlled voltage source is a TwoPort. The right port voltage v2 is controlled by the left port voltage v1 via
v2 = v1 * gain.
The left port current is zero. Any voltage gain can be chosen.
| Name | Default | Description |
|---|---|---|
| gain | 1 | Voltage gain |
model VCV "Linear voltage-controlled voltage source" extends Interfaces.TwoPort; parameter Real gain=1 "Voltage gain"; equation v2 = v1*gain; i1 = 0; end VCV;
Modelica.Electrical.Analog.Basic.VCC
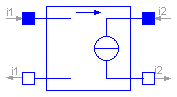
The linear voltage-controlled current source is a TwoPort. The right port current i2 is controlled by the left port voltage v1 via
i2 = v1 * transConductance.
The left port current is zero. Any transConductance can be chosen.
| Name | Default | Description |
|---|---|---|
| transConductance | 1 | Transconductance [S] |
model VCC "Linear voltage-controlled current source" extends Interfaces.TwoPort; parameter SI.Conductance transConductance=1 "Transconductance"; equation i2 = v1*transConductance; i1 = 0; end VCC;
Modelica.Electrical.Analog.Basic.CCV
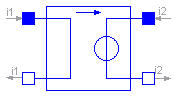
The linear current-controlled voltage source is a TwoPort. The right port voltage v2 is controlled by the left port current i1 via
v2 = i1 * transResistance.
The left port voltage is zero. Any transResistance can be chosen.
| Name | Default | Description |
|---|---|---|
| transResistance | 1 | Transresistance [Ohm] |
model CCV "Linear current-controlled voltage source" extends Interfaces.TwoPort; parameter SI.Resistance transResistance=1 "Transresistance"; equation v2 = i1*transResistance; v1 = 0; end CCV;
Modelica.Electrical.Analog.Basic.CCC
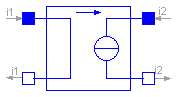
The linear current-controlled current source is a TwoPort. The right port current i2 is controlled by the left port current i1 via
i2 = i1 * gain.
The left port voltage is zero. Any current gain can be chosen.
| Name | Default | Description |
|---|---|---|
| gain | 1 | Current gain |
model CCC "Linear current-controlled current source" extends Interfaces.TwoPort; parameter Real gain=1 "Current gain"; equation i2 = i1*gain; v1 = 0; end CCC;
Modelica.Electrical.Analog.Basic.OpAmp
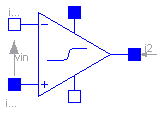
The OpAmp is a simle nonideal model with a smooth out.v = f(vin) characteristic, where "vin = in_p.v - in_n.v". The characteristic is limited by VMax.v and VMin.v. Its slope at vin=0 is the parameter Slope, which must be positive. (Therefore, the absolute value of Slope is taken into calculation.)
| Name | Default | Description |
|---|---|---|
| Slope | 1 | Slope of the out.v/vin characteristic at vin=0 |
model OpAmp "Simple nonideal model of an OpAmp with limitation"
parameter Real Slope=1 "Slope of the out.v/vin characteristic at vin=0";
Modelica.Electrical.Analog.Interfaces.PositivePin in_p
"Positive pin of the input port";
Modelica.Electrical.Analog.Interfaces.NegativePin in_n
"Negative pin of the input port";
Modelica.Electrical.Analog.Interfaces.PositivePin out "Output pin";
Modelica.Electrical.Analog.Interfaces.PositivePin VMax
"Positive output voltage limitation";
Modelica.Electrical.Analog.Interfaces.NegativePin VMin
"Negative output voltage limitation";
SI.Voltage vin "input voltagae";
protected
Real f "auxiliary variable";
Real absSlope;
equation
in_p.i = 0;
in_n.i = 0;
VMax.i = 0;
VMin.i = 0;
vin = in_p.v - in_n.v;
f = 2/(VMax.v - VMin.v);
absSlope = if (Slope < 0) then -Slope else Slope;
out.v = (VMax.v + VMin.v)/2 + absSlope*vin/(1 + absSlope*noEvent(if (f*vin <
0) then -f*vin else f*vin));
end OpAmp;