Learning Probabilistic Graphical Models of
Gene Networks and Fault Networks
Jose M. Peña
ADIT, IDA, LiU, Sweden
Updated 14/03/2011
1
Background and Industrial Motivation
Most if not all
diseases are not determined by a single factor, but rather by a network of
interacting genetic and environmental factors. Knowledge about such a network
would allow to develop better early diagnostics and
drugs. Recent progress in measurement technology has made it possible to
measure gene expression, which enables to compose a rich profile of patients by
combining gene expression, clinical and life-style data. The challenge is now
to develop sound methodologies for learning the referred network from these
measurements. An analogous challenge appears in fault diagnosis. For instance,
trucks are expensive items and diagnosing the cause of a fault in the light of
some sensor measurements may result in huge savings. However, some faults may
cause other faults and even affect the sensors’ outputs. Therefore, learning
the network of interacting faults and sensors may result in more accurate fault
diagnosis. The motivation of the present project is to address these challenges
by modeling the referred networks as Bayesian networks
(BNs) and learning them automatically from historical data.
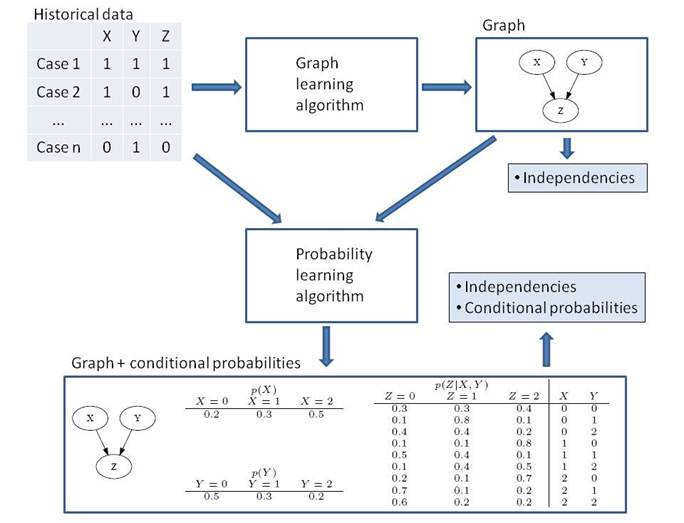
Let U denote a set of
random variables, each of which represents a measurement, e.g. the state of a
gene or a sensor. A BN for U represents a probability distribution for U
through the factorization p(U) = ∏ X in U p(X|Parents(X)), where p(X|Parents(X))
is a conditional probability distribution for X given its parents in a directed
acyclic graph G whose nodes are U (Y is a parent of X if Y → X in G).
When U is discrete, p(X|Parents(X))
is a discrete probability distribution over X for each state of Parents(X).
When U is continuous, p(X|Parents(X))
is typically a Gaussian probability distribution over X whose mean depends
linearly on the value of Parents(X). See the figure above (bottom box) for an
example. The lack of an edge between two random variables in G means that the
two random variables are independent in p(U) given
some other random variables. For instance, some measurements may make some
other measurements irrelevant for predicting the disease or fault. Which random
variables make two non-adjacent random variables independent can be found from
G via a graphical criterion known as d-separation. These
independencies entailed by G enable us to efficiently compute probabilities
such as p(V|W) for any subsets V and W of U without having to resort to the
definition p(V|W) = ∑ U\{V,W} p(U) / ∑ U\W
p(U). For instance, p(V|W) could be the probability of a patient being in a
particular disease stage (V) given the results of some clinical or genetic
tests (W), or the probability of a fault to be present (V) given the readings
of some sensors (W). Learning a BN from some historical data
boils down to first learning the graph representing the independencies in the
data and, then, estimating the corresponding conditional probability
distributions from the data. The second step is typically solved by just
counting frequencies and, thus, we focus in this project on the first step,
which is known to be NP-hard. The learning process is depicted in the figure
above.
BNs
are the most popular member of the so-called probabilistic graphical
models (PGMs), which all share with BNs the principle of representing the
independence structure of a probability distribution by a graph that, later, is
parameterized to allow computing probabilities of interest. PGMs arose in the
70s at the intersection of computer science and statistics. Since then, they
have become one of the most popular paradigms for data analysis and decision
support in many domains. See, for instance, www.hugin.com/case-stories for
some case studies. Besides BNs, other distinguished PGMs are Markov networks
(MNs), which are based on undirected graphs, and chain graphs (CGs), which are
based on graphs with both directed and undirected edges and, thus, encompass
BNs and MNs. This
project aims at studying CGs, from their expressive power to learning
algorithms and their application to modeling gene networks and fault networks.
2 Results
The results of the
project so far consist in having solved, totally or partially, the following
three problems:
1.
Faithfulness: The independence
model represented by a CG is the set of independencies represented according to
c-separation (a graphical criterion analogous to d-separation). I have shown in
[4] that only a tiny fraction of the independence models that can be
represented by CGs seem to be exactly representable by BNs and MNs. Therefore,
the former models would be much more expressive than the latter if there existed a probability distribution that is faithful to each
CG, i.e. a probability distribution that satisfies all and only the
independencies in the CG. CGs without faithful probability distributions are uninteresting because they do not represent valid solutions
(recall that the bottom line is to use CGs as proxies of probability
distributions). The first result of this project is that the faithfulness
question has a positive answer: I have proven that every CG has both discrete
and Gaussian probability distributions that are faithful to it. These results
have been reported in the following two publications:
·
Peña,
J. M. (2009). Faithfulness in Chain Graphs: The Discrete Case. International Journal of Approximate Reasoning, 50 (8),
1306-1313.
·
Peña,
J. M. (2011). Faithfulness
in Chain Graphs: The Gaussian Case. In Proceedings of
the 14th International Conference on Artificial Intelligence and Statistics (AISTATS
2011)
2.
Dependencies: Even if a
probability distribution that is faithful to the CG learnt exists, we cannot
know if that is the one underlying the learning data: It may be that the
distribution underlying the learning data is not faithful to any graph and,
thus, the learning algorithm has simply returned the graph that best
approximates the distribution. Therefore, the arcs in the graph learnt do not
necessarily imply dependencies. Can we develop a graphical criterion for
reading dependencies off the graph instead of independencies
? Humans are typically more interested in discovering dependencies
between measurements: For instance, discovering that the state of some genes
(faults) is informative about that of some other genes (faults) may lead the
biologist (engineer) to hypothesize causal relations. In the past, I have
studied this problem for MNs [5] and BNs [3]. In this project, I would like to
extend these results to CGs. The following two articles, which are a result of
this project, are an intermediate step towards that goal:
·
Peña,
J. M. (2010). Reading Dependencies from Polytree-Like
Bayesian Networks Revisited.
In
Proceedings of the 5th European Workshop on Probabilistic Graphical Models (PGM
2010), 225-232.
·
Peña,
J. M. (2010). Reading
Dependencies from Covariance Graphs. Submitted.
3.
Consensus: Suppose that
multiple experts or learning algorithms provide us with alternative CG models
of a domain, and that we are interested in combining them into a single
consensus CG. Specifically, we are interested in that the consensus CG only
represents independences all the given CGs agree upon and as many of them as
possible. The following article, which is a result of this project, studies the
consensus problem for BNs:
·
Peña, J. M.
(2011). Finding Consensus DAGs.
Submitted.
In particular, the
paper above proves that there may exist several
non-equivalent consensus BNs and that finding one of them is NP-hard. Thus, one
has to resort to heuristics to find an approximated consensus BN. The paper
above proposes a justified heuristic.
3 Ongoing Work
The main lines of current
ongoing research are the following ones:
1.
Dependencies: Extending the
results discussed above, first, to unrestricted BNs and, then, to CGs.
2.
Consensus: Extending the
results discussed above to CGs.
3.
Learning: After having
devoted most of the effort so far to the study of the semantics and expressiveness
of CGs, the next natural challenge is to develop algorithms for learning CGs
from data. Some algorithms already exist but they are not particularly
efficient and, moreover, they are based upon strong assumptions. I am working
on this problem in collaboration with Dr. Jens D. Nielsen, a postdoctoral
researcher in the University of Castilla-La Mancha
(Spain). Dag Sonntag, a recently recruited PhD student working under my
supervision at ADIT, has joined us in this effort. The plan is to extend our BN
learning algorithm in [2] to learn CGs from data. In addition to an
experimental evaluation of the algorithm, we would like to prove that the
algorithm is theoretically correct/consistent under mild
assumptions. I believe the latter is a key feature of any well-founded learning
algorithm.
In
parallel, I am investigating alternative methods for learning CGs from data. I
am working on this together with Juan Ignacio Barba, a PhD student at the University
of Castilla-La Mancha (Spain) who visited ADIT for
four months in the second half of 2010. The visit was very productive and we
succeeded in adapting his BN learning algorithm in [1] to learn CGs from data.
This approach is radically different from the one described in the paragraph
above, because the search for the best CG is not carried out in the space of
CGs but in the space of orderings of the nodes. The reason is that the space of
orderings is smaller and that learning the optimal CG for a given ordering is
simple. We are in the process of writing an article on this.
References
1.
Alonso-Barba,
J. I., delaOssa, L. and Puerta,
J. M. (2010). Structural Learning of Bayesian Networks Using Local Algorithms
Based on the Space of Orderings. Soft Computing, to appear
2.
Nielsen, J. D., Kocka,
T. and Peña, J. M. (2003). On Local Optima in Learning Bayesian Networks. In Proceedings
of the 19th Conference on Uncertainty in Artificial Intelligence (UAI 2003),
435-442.
3.
Peña, J. M. (2007). Reading Dependencies from Polytree-Like
Bayesian Networks. In Proceedings of the 23rd Conference on Uncertainty
in Artificial Intelligence (UAI 2007), 303-309. Errata.
4.
Peña, J. M. (2007). Approximate Counting of Graphical Models Via MCMC. In Proceedings of the 11th International
Conference on Artificial Intelligence and Statistics (AISTATS 2007),
352-359. Software.
5.
Peña, J. M., Nilsson, R., Björkegren,
J. and Tegnér, J. (2009). An Algorithm for Reading
Dependencies from the Minimal Undirected Independence Map of a Graphoid that Satisfies Weak Transitivity. Journal of Machine
Learning Research, 10, 1071-1094.