HyLibLight.Components.Basic.LamResNoStates
HyLibLight.Components.Basic.LamResNoStates
LamResNoStates describes the laminar flow through a component. q = G*dp q flow rate G conductance, m^3/(s * Pa) dp pressure drop across resistance Equations to calculate the conductance G are given in the manual for several components. A conductance of G = 4.167e-13 m^3/s/Pa leads to a flow rate of 1 l/min at 4e7 Pa (=400 bar). As the critical Reynolds number depends on the component there is no check whether the flow is actually laminar or turbulent. See also: OrificeNoStates: The model based on the loss coefficient K describes both flow regimes, laminar for very small Reynolds numbers, turbulent for higher Reynolds numbers (default model). OriPolyNoStates: The model describes both flow regimes, using a interpolation polynomial. OriCavNoStates: Orifice model checking for cavitation. SimOriNoStates: Texbook model, using a constant discharge coefficient (valid for turbulent flow only). MeteringOriNoStates: Metering Orifice, i. e. model OrificeNoStates with variable diameter. TwoOrifices: Two orifices in series, one with variable the other with fixed flow area. OrificeN: Same as OrificeNoStates, but equations rearranged to compute dp for given q. Release Notes: -------------- 1999 - 10 - 24: tested
| Name | Default | Description |
|---|---|---|
| G | 4.2e-13 | conductance of laminar resistance [m3/(s*Pa)] |
model LamResNoStates "Resistance with laminar flow."
extends HyLibLight.Interfaces.TwoPortComp;
parameter HyLibLight.Interfaces.HyLibUnits.Conductance G=4.2e-13
"conductance of laminar resistance";
equation
q = G*dp;
end LamResNoStates;
Basic models of valves. Flow and Pressure Control Valves -------------------------------- These valves control the flow or pressure. They are modelled as static systems. These models have no state variables. CheckValveNoStates: Ideal spring-loaded check valve with laminar/turbulent flow. CheckValveTwoNoStates: Ideal spring-loaded check valve with laminar/turbulent flow (different characteristics). ShuttleValveNoStates: Ideal shuttle valve with internal resistance (static model). ReducingValveNoStates: Ideal pressure reducing valve (static model). SerFlowContNoStates: Ideal series flow control valve (static model). Spool Valves ------------ These valves control the flow according to the position of the spool. The spool dynamics is modelled as a second order system with limits for the spool velocity and position. There are no lumped volumes connected at the ports. ServoValveNoStates: Valve with second order spool dynamics and nonlinearities. Flow area depends linearly on spool position. PropValveNoStates: Valve with second order spool dynamics and nonlinearities. Flow area depends not linearly on spool position, usually large overlap.
HyLibLight.Components.Basic.ReliefValveNoStates
Ideal model of a relief valve
The resistance depends on the pressure differential dp = port_A.p - port_B.p
1) dp < pclosed => valve closed, only leakage
q = dp * GLeak
2) pclosed < dp < popen => working range,
i. e. valve partially opened
3) popen < dp => valve wide open
q = dp * GOpen
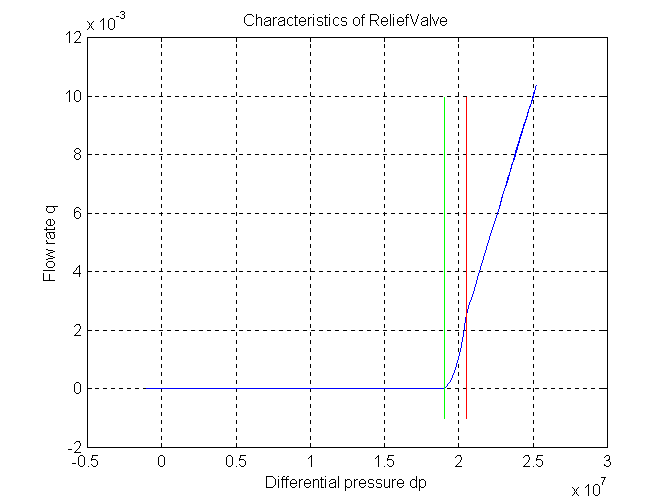
parameters for figure: pclosed = 190e5 Pa popen = 205e5 Pa GLeak = 1.11e-12 m^3/(s*Pa) GOpen = 1.666e-9 m^3/(s*Pa) Release Notes: -------------- 1999 - 11 - 16: tested
| Name | Default | Description |
|---|---|---|
| pclosed | 190e5 | valve closed if dp smaller [Pa] |
| popen | 205e5 | valve wide open if dp higher [Pa] |
| GLeak | 1.111e-12 | conductance of closed valve, i. e. leakage [m3/(s*Pa)] |
| GOpen | 1.666e-9 | conductance of wide open valve [m3/(s*Pa)] |
model ReliefValveNoStates "Ideal model of a relief valve."
extends HyLibLight.Interfaces.TwoPortComp;
parameter Modelica.SIunits.Pressure pclosed(final min=0) = 190e5
"valve closed if dp smaller";
parameter Modelica.SIunits.Pressure popen=205e5
"valve wide open if dp higher";
parameter HyLibLight.Interfaces.HyLibUnits.Conductance GLeak=1.111e-12
"conductance of closed valve, i. e. leakage";
parameter HyLibLight.Interfaces.HyLibUnits.Conductance GOpen=1.666e-9
"conductance of wide open valve";
Boolean closed(start=false)
"closed: .true. => valve closed, only leakage";
Boolean open(start=false) "open : .true. => valve wide open";
equation
closed = dp < pclosed;
open = dp > popen;
q = if closed then dp*GLeak else if open then (dp - pclosed)*GOpen + dp*
GLeak else (dp - pclosed)^2*GOpen/(popen - pclosed) + dp*GLeak;
assert(popen > pclosed,
"Parameter popen MUST be greater than parameter pclosed.");
end ReliefValveNoStates;
HyLibLight.Components.Basic.CheckValveNoStates
Spring-loaded check valve with laminar/turbulent flow
The resistance depends on the pressure differential
1) pressure differential dp < p_closed
=> q = dp * GLeak
leakage from high pressure port to low pressure port only
2) p_closed < dp < p_open
=> valve is partially open
3) dp > p_open
=> valve is wide open,
flow mode depends on Reynolds number
resistance modelled as orifice parallel with laminar
resistance (leakage)
The mass and flow forces are not included.
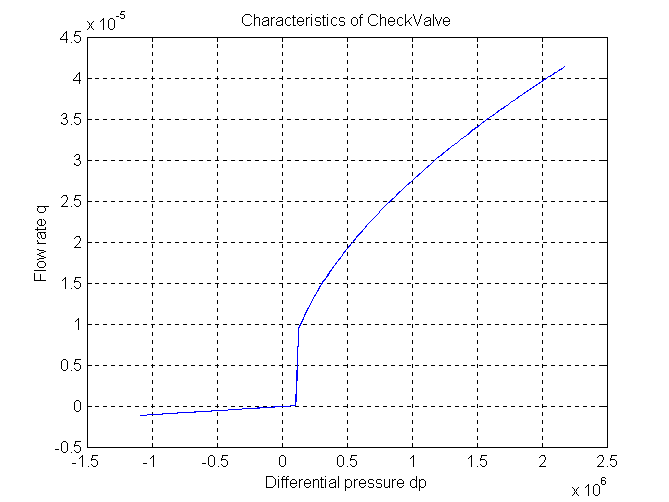
parameters for figure: pclosed = 1e5 Pa popen = 1.25e5 Pa diameter = 1e-3 GLeak=1.e-12 (very high value, for demonstration only) k1=10. k2=2. Release Notes: -------------- 1999 - 11 - 16: tested
| Name | Default | Description |
|---|---|---|
| pclosed | 1e5 | pressure to start opening the valve [Pa] |
| popen | 1.25e5 | pressure to open valve completely [Pa] |
| diameter | 1.e-3 | diameter of equivalent orifice [m] |
| GLeak | 1.e-12 | conductance of leakage [m3/(s*Pa)] |
| k1 | 10. | laminar part [ ] |
| k2 | 2. | tubulent part, k2 = 1 / C_d^2 [ ] |
model CheckValveNoStates
"Spring-loaded check valve with laminar/turbulent flow."
extends HyLibLight.Components.Basic.CheckValvePartial;
parameter Modelica.SIunits.Pressure pclosed(final min=0) = 1e5
"pressure to start opening the valve";
parameter Modelica.SIunits.Pressure popen(final min=0) = 1.25e5
"pressure to open valve completely";
parameter Modelica.SIunits.Diameter diameter=1.e-3
"diameter of equivalent orifice";
parameter HyLibLight.Interfaces.HyLibUnits.Conductance GLeak=1.e-12
"conductance of leakage";
parameter Real k1=10. "laminar part [ ]";
parameter Real k2=2. "tubulent part, k2 = 1 / C_d^2 [ ]";
Boolean closed(start=false) "valve closed, only leakage";
Boolean open(start=false) "valve wide open";
Real bopen;
Modelica.SIunits.VolumeFlowRate qopen;
equation
closed = dp < pclosed;
open = dp > popen;
qopen = (sqrt(k1^2*nu^2*rho^2 + 8*diameter^2*k2*noEvent(abs(popen))*rho) -
k1*nu*rho)*diameter*Modelica.Constants.pi/(8*k2*rho);
bopen = qopen/(popen - pclosed);
port_A.q = if closed then dp*GLeak else if open then (sqrt(k1^2*nu^2*rho^2
+ 8*diameter^2*k2*noEvent(abs(dp))*rho) - k1*nu*rho)*diameter*Modelica.
Constants.pi/(8*k2*rho) + dp*GLeak else (dp - pclosed)^2*bopen/(popen -
pclosed) + dp*GLeak;
assert(popen > pclosed,
"Parameter popen MUST be greater than parameter pclosed.");
end CheckValveNoStates;
HyLibLight.Components.Basic.VolumePartial
Partial model of a lumped volume, i. e. graphical information
model VolumePartial "Partial model of a lumped volume" extends HyLibLight.Interfaces.OnePortCompInput; end VolumePartial;
HyLibLight.Components.Basic.LineMiddle
Class LineMiddle contains the equations for an element
between the entrance and the exit element.
The connectors are used to connect this element to another middle
element of A to an entrance of B to an Exit element.
| Name | Default | Description |
|---|---|---|
| ElementLength | length of one element [m] | |
| diameter | line diameter [m] | |
| aSound | speed of sound in oil [m/s] |
model LineMiddle "Line element between entrance and exit." extends HyLibLight.Components.Basic.LineBase; equation der(pk) = aSound/ElementLength*Zc*(qkminus - qkplus); end LineMiddle;
HyLibLight.Components.Basic.LineEntrance
Class LineEntrance contains the equations for the entrance
element, i. e. the beginning, of a long line.
port_A is used to connect the long line to another
hydraulic component.
| Name | Default | Description |
|---|---|---|
| ElementLength | length of one element [m] | |
| diameter | line diameter [m] | |
| aSound | speed of sound in oil [m/s] |
model LineEntrance "Entrance element of a long line." extends HyLibLight.Components.Basic.LineBase; Real ReynoldsNumber "Reynlods number"; equation ReynoldsNumber = qkminus*4/(diameter*Modelica.Constants.pi*nu); der(pk) = 2*aSound/ElementLength*Zc*(qkminus - qkplus); end LineEntrance;
HyLibLight.Components.Basic.LineExit
Class LineExit contains the equations for the exit
element, i. e. the end, of a long line.
Connector port_B is used to connect the long line to another
hydraulic component.
| Name | Default | Description |
|---|---|---|
| ElementLength | length of one element [m] | |
| diameter | line diameter [m] | |
| aSound | speed of sound in oil [m/s] |
model LineExit "Exit element of a long line." extends HyLibLight.Components.Basic.LineBase; Real ReynoldsNumber "Reynlods number"; equation der(pk) = 2*aSound/ElementLength*Zc*(qkminus - qkplus); ReynoldsNumber = qkminus*4/(diameter*Modelica.Constants.pi*nu); end LineExit;
HyLibLight.Components.Basic.CheckValvePartial
Partial model of a check valve, i. e. graphical information.
model CheckValvePartial "Partial model of a check valve, i. e. graphical information." extends HyLibLight.Interfaces.TwoPortComp; replaceable model Prop extends HyLibLight.Interfaces.FluidProp; end Prop; extends Prop; end CheckValvePartial;
HyLibLight.Components.Basic.LineBase
Class LineBase contains the equations and parameters
that are needed for all long line classes.
| Name | Default | Description |
|---|---|---|
| ElementLength | length of one element [m] | |
| diameter | line diameter [m] | |
| aSound | speed of sound in oil [m/s] |
model LineBase "Base class for long line classes."
replaceable model Prop extends HyLibLight.Interfaces.FluidProp; end Prop;
extends Prop;
constant Real k1=0.1918;
constant Real k2=0.0948;
constant Real k3=0.0407;
constant Real tau1=0.2496;
constant Real tau2=0.0352;
constant Real tau3=0.0024;
Real alpha;
Real Zc;
Real wk1;
Real wk2;
Real wk3;
parameter Modelica.SIunits.Length ElementLength
"length of one element";
parameter Modelica.SIunits.Diameter diameter "line diameter";
parameter Modelica.SIunits.VelocityOfSound aSound
"speed of sound in oil";
Modelica.SIunits.Pressure pk;
Modelica.SIunits.Pressure pkplus;
Modelica.SIunits.VolumeFlowRate qkminus;
Modelica.SIunits.VolumeFlowRate qkplus;
HyLibLight.Interfaces.Port_A port_A
"Port A, were oil flows into the component (positive q, port_A.p > port_B.p means positive dp)"
;
HyLibLight.Interfaces.Port_B port_B
"Port A, were oil leaves the component (negative q, port_A.p > port_B.p means positive dp)"
;
equation
pk = port_A.p;
pkplus = port_B.p;
qkminus = port_A.q;
qkplus = -port_B.q;
alpha = 32*nu/diameter^2;
Zc = aSound*rho/(diameter^2*Modelica.Constants.pi/4);
der(wk1) = alpha*k1/tau1^2*Zc*qkplus - alpha/tau1*wk1;
der(wk2) = alpha*k2/tau2^2*Zc*qkplus - alpha/tau2*wk2;
der(wk3) = alpha*k3/tau3^2*Zc*qkplus - alpha/tau3*wk3;
der(qkplus) = 1/Zc*(aSound/ElementLength*(pk - pkplus) - alpha*(1 + k1/tau1
+ k2/tau2 + k3/tau3)*Zc*qkplus + alpha*(wk1 + wk2 + wk3));
end LineBase;
HyLibLight.Components.Basic.AccumulatorPartial
Partial model of an accumulator, i. e. graphical information
model AccumulatorPartial "Partial model of an accumulator" end AccumulatorPartial;
HyLibLight.Components.Basic.ValveLogic
Switching logic for valve
| Name | Default | Description |
|---|---|---|
| pprecharge | 50e5 |
model ValveLogic "Switching logic for valve"
parameter Real pprecharge=50e5;
Modelica.Blocks.Interfaces.InPort inPort1(final n=1)
"Connector of input signal used as flow rate";
Modelica.Blocks.Interfaces.InPort inPort2(final n=1)
"Connector of input signal used as flow rate";
Modelica.Blocks.Interfaces.OutPort outPort(final n=1);
equation
outPort.signal[1] = if (inPort1.signal[1] > pprecharge or inPort2.signal[
1] > pprecharge) then 1 else 0;
end ValveLogic;
HyLibLight.Components.Basic.CheckValvePartial.Prop
replaceable model Prop extends HyLibLight.Interfaces.FluidProp;end Prop;
HyLibLight.Components.Basic.LineBase.Prop
replaceable model Prop extends HyLibLight.Interfaces.FluidProp;end Prop;