


This package contains the following basic mathematical functions:
sin(u) sine cos(u) cosine tan(u) tangent (u shall not be -pi/2, pi/2, 3*pi/2, ...) asin(u) inverse sine (-1 <= u <= 1) acos(u) inverse cosine (-1 <= u <= 1) atan(u) inverse tangent atan2(u1,u2) four quadrant inverse tangent sinh(u) hyperbolic sine cosh(u) hyperbolic cosine tanh(u) hyperbolic tangent exp(u) exponential, base e log(u) natural (base e) logarithm (u > 0) log10(u) base 10 logarithm (u > 0)
These functions are used by calling them directly with a full name (e.g. y = Modelica.Math.asin(0.5)).
Release Notes:
Copyright © 1999-2002, Modelica Association and DLR.
The Modelica package is free software; it can be redistributed and/or modified under the terms of the Modelica license, see the license conditions and the accompanying disclaimer in the documentation of package Modelica in file "Modelica/package.mo".
![]()
partial function baseIcon1 "Basic icon for mathematical function with y-axis on left side" end baseIcon1;
![]()
partial function baseIcon2 "Basic icon for mathematical function with y-axis in middle" end baseIcon2;
 Modelica.Math.sin
Modelica.Math.sin
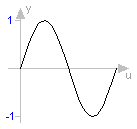
function sin "sine" extends baseIcon1; input SI.Angle u; output Real y; external "C" y = sin(u); end sin;
 Modelica.Math.cos
Modelica.Math.cos
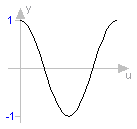
function cos "cosine" extends baseIcon1; input SI.Angle u; output Real y; external "C" y = cos(u); end cos;
 Modelica.Math.tan
Modelica.Math.tan
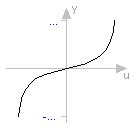
function tan "tangent (u shall not be -pi/2, pi/2, 3*pi/2, ...)" extends baseIcon2; input SI.Angle u; output Real y; external "C" y = tan(u); end tan;
 Modelica.Math.asin
Modelica.Math.asin
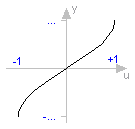
function asin "inverse sine (-1 <= u <= 1)" extends baseIcon2; input Real u; output SI.Angle y; external "C" y = asin(u); end asin;
 Modelica.Math.acos
Modelica.Math.acos
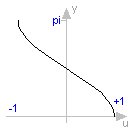
function acos "inverse cosine (-1 <= u <= 1)" extends baseIcon2; input Real u; output SI.Angle y; external "C" y = acos(u); end acos;
 Modelica.Math.atan
Modelica.Math.atan
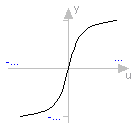
function atan "inverse tangent" extends baseIcon2; input Real u; output SI.Angle y; external "C" y = atan(u); end atan;
 Modelica.Math.atan2
Modelica.Math.atan2
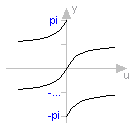
function atan2 "four quadrant inverse tangent" extends baseIcon2; input Real u1; input Real u2; output SI.Angle y; external "C" y = atan2(u1, u2); end atan2;
 Modelica.Math.sinh
Modelica.Math.sinh
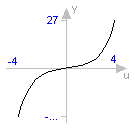
function sinh "hyperbolic sine" extends baseIcon2; input Real u; output Real y; external "C" y = sinh(u); end sinh;
 Modelica.Math.cosh
Modelica.Math.cosh
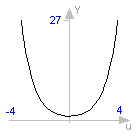
function cosh "hyperbolic cosine" extends baseIcon2; input Real u; output Real y; external "C" y = cosh(u); end cosh;
 Modelica.Math.tanh
Modelica.Math.tanh
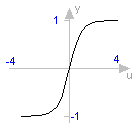
function tanh "hyperbolic tangent" extends baseIcon2; input Real u; output Real y; external "C" y = tanh(u); end tanh;
 Modelica.Math.exp
Modelica.Math.exp
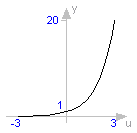
function exp "exponential, base e" extends baseIcon2; input Real u; output Real y; external "C" y = exp(u); end exp;
 Modelica.Math.log
Modelica.Math.log
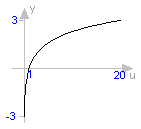
function log "natural (base e) logarithm (u shall be > 0)" extends baseIcon1; input Real u; output Real y; external "C" y = log(u); end log;
 Modelica.Math.log10
Modelica.Math.log10
function log10 "base 10 logarithm (u shall be > 0)" extends baseIcon1; input Real u; output Real y; external "C" y = log10(u); end log10;
 Modelica.Math.tempInterpol1
Modelica.Math.tempInterpol1
function tempInterpol1
"temporary routine for linear interpolation (will be removed)"
input Real u "input value (first column of table)";
input Real table[:, :] "table to be interpolated";
input Integer icol "column of table to be interpolated";
output Real y "interpolated input value (icol column of table)";
protected
Integer i;
Integer n "number of rows of table";
Real u1;
Real u2;
Real y1;
Real y2;
algorithm
n := size(table, 1);
if n <= 1 then
y := table[1, icol];
else
// Search interval
if u <= table[1, 1] then
i := 1;
else
i := 2;
// Supports duplicate table[i, 1] values
// in the interior to allow discontinuities.
// Interior means that
// if table[i, 1] = table[i+1, 1] we require i>1 and i+1<n
while i < n and u >= table[i, 1] loop
i := i + 1;
end while;
i := i - 1;
end if;
// Get interpolation data
u1 := table[i, 1];
u2 := table[i + 1, 1];
y1 := table[i, icol];
y2 := table[i + 1, icol];
assert(u2 > u1, "Table index must be increasing");
// Interpolate
y := y1 + (y2 - y1)*(u - u1)/(u2 - u1);
end if;
end tempInterpol1;
 Modelica.Math.tempInterpol2
Modelica.Math.tempInterpol2
function tempInterpol2
"temporary routine for vectorized linear interpolation (will be removed)"
input Real u "input value (first column of table)";
input Real table[:, :] "table to be interpolated";
input Integer icol[:] "column(s) of table to be interpolated";
output Real y[1, size(icol, 1)]
"interpolated input value(s) (column(s) icol of table)";
protected
Integer i;
Integer n "number of rows of table";
Real u1;
Real u2;
Real y1[1, size(icol, 1)];
Real y2[1, size(icol, 1)];
algorithm
n := size(table, 1);
if n <= 1 then
y := transpose([table[1, icol]]);
else
// Search interval
if u <= table[1, 1] then
i := 1;
else
i := 2;
// Supports duplicate table[i, 1] values
// in the interior to allow discontinuities.
// Interior means that
// if table[i, 1] = table[i+1, 1] we require i>1 and i+1<n
while i < n and u >= table[i, 1] loop
i := i + 1;
end while;
i := i - 1;
end if;
// Get interpolation data
u1 := table[i, 1];
u2 := table[i + 1, 1];
y1 := transpose([table[i, icol]]);
y2 := transpose([table[i + 1, icol]]);
assert(u2 > u1, "Table index must be increasing");
// Interpolate
y := y1 + (y2 - y1)*(u - u1)/(u2 - u1);
end if;
end tempInterpol2;