ObjectStab.Network.Partials

ObjectStab.Network.Partials.BusBase

Information

Defines the voltage amplitude and phase.

Modelica definition

partial model BusBase "Shell model for busbar definitions" 
  Base.VoltageAmplitude V(start=1) "Voltage Amplitude";
  Base.VoltageAngle delta "Voltage Angle";
  
  ObjectStab.Base.Pin T;
equation 
  V = sqrt((1 + T.va)*(1 + T.va) + T.vb*T.vb);
  delta = atan(T.vb/(1 + T.va))*180/Modelica.Constants.PI;
end BusBase;

ObjectStab.Network.Partials.PilinkBase

Parameters

Name	Default	Description
R	0.0	Series Resistance [p.u.]
X	0.1	Series Reactance [p.u.]
B	0.1	Shunt Susceptance [p.u.]
G	0.0	Shunt Conductance [p.u.]

Modelica definition

partial model PilinkBase "Pilink" 
  extends Base.TwoPin;
  parameter Base.Resistance R=0.0 "Series Resistance";
  parameter Base.Reactance X=0.1 "Series Reactance";
  parameter Base.Susceptance B=0.1 "Shunt Susceptance";
  parameter Base.Conductance G=0.0 "Shunt Conductance";
end PilinkBase;

ObjectStab.Network.Partials.ImpTransformer

Information

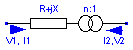
Shell model for with leakage reactance and impedance transformers 
according to [1, pp.54-55]:


           R+jX
           ----   n:1
V1, I1  ---    ---()-| V2, I2
    ->     ----        <- 

  


The resulting expressions for the nodal current injections can
be written:

I1 = Yt*V1                           -n*Yt*V2
I2 = -conjugate(n)*Yt*V1+conjugate(n)*n*Yt*V2


The model does NOT incorporate active or reactive losses due to the 
excitation current, or transformer phase shift. 

---
[1] J. Machowski, J.W. Bialek, and J.R. Bumby, Power System Dynamics 
and Stability, Number ISBN 0-471-97174. Wiley, 1993.

Parameters

Name	Default	Description
R	0.0	Leakage Resistance [p.u.]
X	0.1	Leakage Reactance [p.u.]

Modelica definition

partial model ImpTransformer "Shell model for transformer" 
  extends Base.TwoPin;
  
  parameter Base.Resistance R=0.0 "Leakage Resistance";
  parameter Base.Reactance X=0.1 "Leakage Reactance";
  
  Base.TapRatio n(start=1) "Tap Ratio";
  
equation 
  T2.ia = n*(-R - R*T1.va - X*T1.vb + n*R + n*R*T2.va + n*X*T2.vb)/(R^2 + X^2)
    ;
  T2.ib = n*(X + X*T1.va - R*T1.vb - n*X - n*X*T2.va + n*R*T2.vb)/(R^2 + X^2);
  T1.ia = -(-R - R*T1.va - X*T1.vb + n*R + n*R*T2.va + n*X*T2.vb)/(R^2 + X^2);
  T1.ib = -(X + X*T1.va - R*T1.vb - n*X - n*X*T2.va + n*R*T2.vb)/(R^2 + X^2);
end ImpTransformer;

ObjectStab.Network.Partials.TCULBase

Information

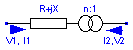
Extends the ImpTransformer model with definitions for time delay
and transformer stepsizes according to [1]. 

The model measures the voltage at it's terminal T1 and compares that to
the voltage reference value Vref. The reulting voltage deviation is then
used as input to the control system.

Using the parameter the characteristics of the mechanical delay time (Tm) and
the controlled delay time (Td) the TCUL can be influenced according
to the table below:

---------------------------------
method|    Td     |    Tm       |  
---------------------------------
  1   |  constant |  constant   |
  2   |  inverse  |  constant   |
  3   |  inverse  |  inverse    | 
  4   |  both     |  constant   | 
---------------------------------

Use the subclasses TCULCon for continuous approximation (more computationally)
efficient or the the subclass TCULDis for the true discrete realization.


---
[1] P.W. Sauer and M.A. Pai, "A comparison of discrete vs. continuous 
dynamic models of tap-changing-under-load transformers", in Proceedings 
of NSF/ECC Workshop on Bulk power System Voltage Phenomena - III : 
Voltage Stability, Security and Control,  Davos, Switzerland, 1994.

Parameters

Name	Default	Description
R	0.0	Leakage Resistance [p.u.]
X	0.1	Leakage Reactance [p.u.]
method	3	Method number
stepsize	0.0167	Step Size [p.u.]
mintap	-8	Minimum tap step [1]
maxtap	8	Maximum tap step [1]
Tm0	10	Mechanical Time Delay [s]
Td0	20	Controller Time Delay 1 [s]
Td1	20	Controller Time Delay 1 [s]
DB	0.03	TCUL Voltage Deadband (double-sided) [p.u.]
Vref	1	TCUL Voltage Reference [p.u.]

Modelica definition

partial model TCULBase "Shell model for TCULs" 
  extends ImpTransformer;
  parameter Integer method=3 "Method number";
  parameter Base.TapRatio stepsize=0.0167 "Step Size";
  parameter Base.TapStep mintap=-8 "Minimum tap step";
  parameter Base.TapStep maxtap=8 "Maximum tap step";
  
  parameter Base.Duration Tm0=10 "Mechanical Time Delay";
  parameter Base.Duration Td0=20 "Controller Time Delay 1";
  parameter Base.Duration Td1=20 "Controller Time Delay 1";
  parameter Base.VoltageAmplitude DB=0.03 
    "TCUL Voltage Deadband (double-sided)";
  parameter Base.VoltageAmplitude Vref=1 "TCUL Voltage Reference";
  
  Integer tappos "Current tap step [number]";
  Base.VoltageAmplitude udev;
equation 
  
  udev = sqrt((1 + T1.va)*(1 + T1.va) + T1.vb*T1.vb) - Vref;
end TCULBase;