ModelicaAdditions.MultiBody.Examples.Loops.Utilities

ModelicaAdditions.MultiBody.Examples.Loops.Utilities.Engine

Information

Use the following settings:

experiment StopTime=0.2 Interval=0.002 Tolerance=1.E-8


Perform 'simulate' and then see animation in
Animation window.

  Plot the following variables:

  AngVelDegS: Angular velocity of motor shaft [rev/min]
  x         : position of cylinder [m]
  press     : pressure in cylinder [bar]

Parameters

Name	Default	Description
D	0.1
e	0.05
L	0.2
Load	20

Modelica definition

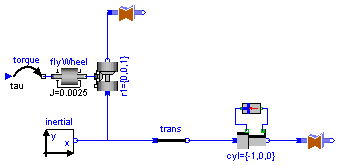
partial model Engine 
  extends Modelica.Icons.Example;
  parameter Real D=0.1;
  parameter Real e=0.05;
  parameter Real L=0.2;
  parameter Real Load=20;
  constant Real PI=Modelica.Constants.pi;
  output Real AngVelDegS;
  output Real x;
  output Real press;
  output Real T;
  output Real V;
  output Real dens;
  MultiBody.Parts.InertialSystem inertial(g=0);
  MultiBody.Joints.Revolute r1(startValueFixed=true, qd(start=-157));
  MultiBody.Joints.Prismatic cyl(n={-1,0,0});
  MultiBody.Parts.FrameTranslation trans(r={sqrt((D/2 + L)^2 - e^2),-e,0});
  MultiBody.Parts.ShapeBody piston(
    r={0.1,0,0}, 
    m=0.3, 
    I33=0.0001, 
    Shape="cylinder", 
    Width=0.05, 
    Height=0.05);
  MultiBody.Parts.ShapeBody crank(
    r={D/2,0,0}, 
    Width=0.01, 
    Height=0.01, 
    Material={0,0,1,0.5});
  MultiBody.Examples.Loops.Utilities.GasForce gasForce(L=(sqrt((L + D/2)^2
         - e^2) - sqrt((L - D/2)^2 - e^2)), d=0.05);
  Modelica.Mechanics.Rotational.Inertia flyWheel(J=0.0025);
  Modelica.Mechanics.Rotational.Torque torque;
equation 
  connect(inertial.frame_b, r1.frame_a);
  connect(inertial.frame_b, trans.frame_a);
  connect(trans.frame_b, cyl.frame_a);
  connect(cyl.frame_b, piston.frame_a);
  connect(cyl.bearing, gasForce.flange_a);
  connect(cyl.axis, gasForce.flange_b);
  connect(flyWheel.flange_b, r1.axis);
  connect(torque.flange_b, flyWheel.flange_a);
  connect(r1.frame_b, crank.frame_a);
  torque.tau = (if r1.qd > 0 then -1 else 1)*Load;
  
  AngVelDegS = -r1.qd*60/(2*PI);
  /*rev/min*/
  
  x = gasForce.s_rel;
  press = gasForce.press;
  T = gasForce.T;
  V = gasForce.V;
  dens = gasForce.dens;
end Engine;

ModelicaAdditions.MultiBody.Examples.Loops.Utilities.GasForce

Parameters

Name	Default	Description
L		Length of cylinder [m]
d		diameter of cylinder [m]
k0	0.01
k1	1
k	1

Modelica definition

model GasForce 
  extends Modelica.Mechanics.Translational.Interfaces.Compliant;
  parameter SIunits.Length L "Length of cylinder";
  parameter SIunits.Length d "diameter of cylinder";
  parameter Real k0=0.01;
  parameter Real k1=1;
  parameter Real k=1;
  constant Real PI=3.14159265;
  SIunits.Position x;
  SIunits.Density dens;
  SIunits.Pressure press "cylinder pressure";
  SIunits.Volume V;
  SIunits.Temperature T;
  SIunits.Velocity v_rel;
equation 
  x = 1 - s_rel/L;
  v_rel = der(s_rel);
  
  press = if v_rel < 0 then (if x < 0.987 then 177.4132*x^4 - 287.2189*x
    ^3 + 151.8252*x^2 - 24.9973*x + 2.4 else 2836360*x^4 - 10569296*x^3 + 
    14761814*x^2 - 9158505*x + 2129670) else (if x > 0.93 then -3929704*x^4
     + 14748765*x^3 - 20747000*x^2 + 12964477*x - 3036495 else 145.930*x^4 - 
    131.707*x^3 + 17.3438*x^2 + 17.9272*x + 2.4);
  
  f = -1.0E5*press*PI*d^2/4;
  
  V = k0 + k1*(1 - x);
  dens = 1/V;
  press*V = k*T;
end GasForce;